library(gamlss)
library(gamlss.ggplots)
library(gamlss.add)
library(ggplot2)
library(dplyr)
library(gamboostLSS)10: Social media post performance
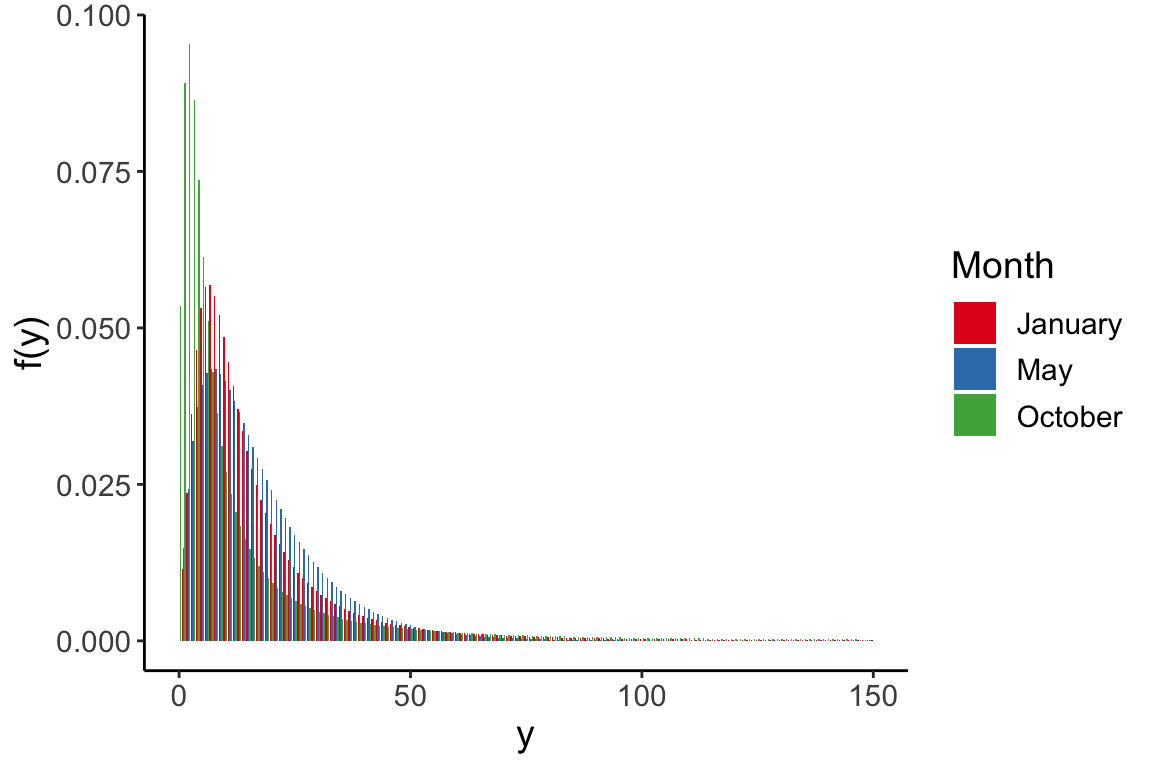
data(fbdata)Figure 10.1
Facebook data: histogram of the number of shares, truncated for display at 100 and overlaid with density estimate.
fbdata %>% dplyr::select(share) %>%
filter(share<101) %>% ## truncate at 100
ggplot(aes(share)) +
geom_histogram(aes(y=after_stat(density)), colour="darkblue", fill="lightblue", binwidth=1) +
theme_bw(base_size=12) +
xlab("Number of shares") +
ylab("Density") +
stat_density(alpha=.2, fill="#FF6666", bw=1.8, outline.type="upper", colour="black")+
theme(axis.text.x=element_text(size=14))+
theme(axis.text.y=element_text(size=14))+
theme(axis.title.x = element_text(size=14),
axis.title.y = element_text(size=14))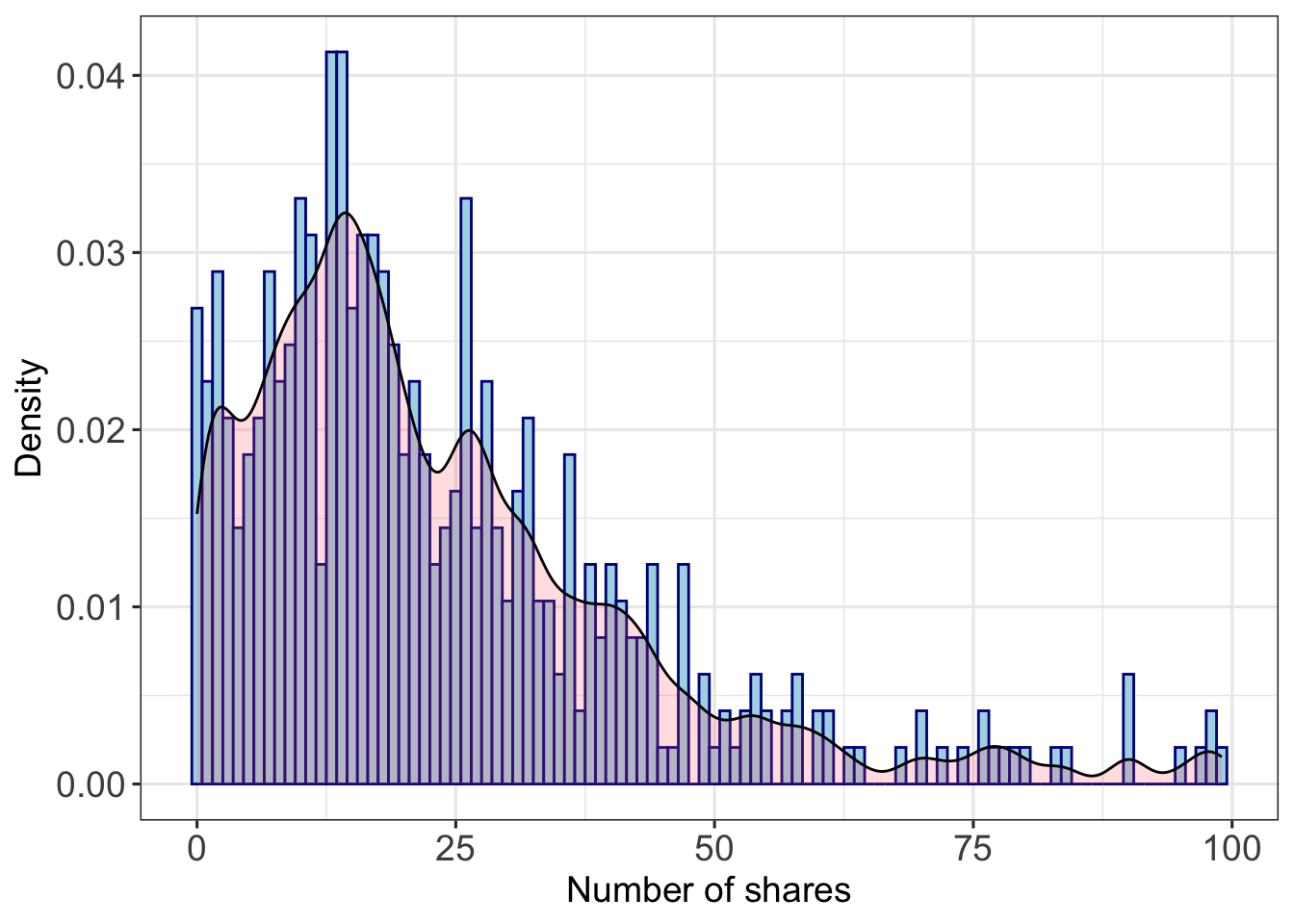
Model building
Select the response distribution
The gamlss cyclic P-spline function
pbc()has been used for the smooth cyclic terms forPost.Hour,Post.WeekdayandPost.Month.Because of numerical instability of the
pbc(Post.Month)term, the number of break points (knots) was set at 5 for this term (inter=5).
m0 <- gamlss(share ~ Category + pbc(Post.Month, control=pbc.control(inter=5)) + pbc(Post.Weekday),
sigma.formula = ~ pbc(Post.Month, control=pbc.control(inter=5)) +
Category + pbc(Post.Weekday),
nu.formula = ~ Category,
tau.formula = ~ Category,
data = fbdata, family=PO)GAMLSS-RS iteration 1: Global Deviance = 14158.62
GAMLSS-RS iteration 2: Global Deviance = 14158.62 T1 <- chooseDist(m0, type="count")minimum GAIC(k= 2 ) family: ZASICHEL
minimum GAIC(k= 3.84 ) family: ZASICHEL
minimum GAIC(k= 6.2 ) family: SI T1[order(T1[,1])[1:5],] ## top 5 in order for AIC 2 3.84 6.2
ZASICHEL 4087.826 4117.266 4155.026
ZISICHEL 4092.669 4122.109 4159.869
ZABNB 4092.753 4122.193 4159.953
SI 4095.530 4119.450 4150.130
SICHEL 4097.770 4121.690 4152.370T1[order(T1[,3])[1:5],] ## top 5 in order for BIC 2 3.84 6.2
SI 4095.530 4119.450 4150.130
SICHEL 4097.770 4121.690 4152.370
ZASICHEL 4087.826 4117.266 4155.026
BNB 4102.025 4125.945 4156.625
ZISICHEL 4092.669 4122.109 4159.869Select covariates
The gamlss function stepGAICAll.A() was used for covariate selection, with the AIC as criterion (the default). The lengthy output of stepGAICAll.A() shown below can be suppressed with the argument trace=FALSE.
# starting model
m1 <- gamlss(share~1, data = fbdata, family=SICHEL, method=mixed(20,100), trace=FALSE)
m.SICHEL <- stepGAICAll.A(m1,
scope=list(lower=~1,
upper = ~ Category + Type + pbc(Post.Weekday) +
pbc(Post.Month, control=pbc.control(inter=5)) +
pbc(Post.Hour) + Paid))---------------------------------------------------
Distribution parameter: mu
Start: AIC= 4280
share ~ 1
Df AIC
+ Category 2.0000 4186.3
+ pbc(Post.Hour) 8.3218 4252.8
+ pbc(Post.Weekday) 1.0000 4266.6
+ Type 2.0000 4272.2
+ Paid 1.0000 4275.0
+ pbc(Post.Month, control = pbc.control(inter = 5)) 1.0000 4278.9
<none> 4280.0
Step: AIC= 4186.32
share ~ Category
Df AIC
+ pbc(Post.Weekday) 1.0000 4168.5
+ pbc(Post.Hour) 1.0003 4184.4
+ pbc(Post.Month, control = pbc.control(inter = 5)) 1.0000 4184.6
<none> 4186.3
+ Paid 1.0000 4186.4
+ Type 2.0000 4189.0
Step: AIC= 4168.46
share ~ Category + pbc(Post.Weekday)
Df AIC
+ pbc(Post.Month, control = pbc.control(inter = 5)) 1.0000 4166.3
+ pbc(Post.Hour) 1.0003 4167.0
<none> 4168.5
+ Paid 1.0000 4170.1
+ Type 2.0000 4171.0
Step: AIC= 4166.25
share ~ Category + pbc(Post.Weekday) + pbc(Post.Month, control = pbc.control(inter = 5))
Df AIC
+ pbc(Post.Hour) 4.5673 4156.3
<none> 4166.3
+ Paid 1.0000 4167.5
+ Type 2.0000 4167.8
Step: AIC= 4156.28
share ~ Category + pbc(Post.Weekday) + pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour)
Df AIC
+ Type 2.2164 4155.3
<none> 4156.3
+ Paid 1.0240 4157.8
Step: AIC= 4155.31
share ~ Category + pbc(Post.Weekday) + pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour) + Type
Df AIC
<none> 4155.3
+ Paid 0.97896 4156.8
---------------------------------------------------
Distribution parameter: sigma
Start: AIC= 4155.31
~1
Df AIC
+ Category 1.14140 4134.8
+ pbc(Post.Month, control = pbc.control(inter = 5)) 1.17363 4147.4
+ pbc(Post.Weekday) 1.01504 4151.0
+ pbc(Post.Hour) 0.62380 4151.8
<none> 4155.3
+ Paid 0.97953 4157.2
+ Type 1.94709 4157.6
Step: AIC= 4134.76
~Category
Df AIC
+ pbc(Post.Month, control = pbc.control(inter = 5)) 1.64616 4127.2
+ pbc(Post.Weekday) 0.85811 4131.8
+ Paid 1.18304 4133.7
+ pbc(Post.Hour) 0.84724 4134.4
<none> 4134.8
+ Type 1.95036 4135.9
Step: AIC= 4127.24
share ~ Category + pbc(Post.Month, control = pbc.control(inter = 5))
Df AIC
+ pbc(Post.Hour) 0.76260 4118.3
+ pbc(Post.Weekday) 0.89129 4123.1
<none> 4127.2
+ Paid 0.98746 4127.9
+ Type 1.89642 4130.1
Step: AIC= 4118.3
share ~ Category + pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour)
Df AIC
+ pbc(Post.Weekday) 0.93208 4113.8
<none> 4118.3
+ Paid 0.98401 4119.1
+ Type 1.99804 4121.5
Step: AIC= 4113.8
share ~ Category + pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour) + pbc(Post.Weekday)
Df AIC
<none> 4113.8
+ Paid 0.96737 4114.6
+ Type 1.99660 4117.7
---------------------------------------------------
Distribution parameter: nu
Start: AIC= 4113.8
~1
Df AIC
+ pbc(Post.Month, control = pbc.control(inter = 5)) -2.2657 4089.5
+ Category -1.2657 4090.7
+ pbc(Post.Hour) -2.2656 4098.6
+ pbc(Post.Weekday) -2.2657 4099.8
+ Paid -2.2656 4108.5
+ Type 2.4285 4110.0
<none> 4113.8
Step: AIC= 4089.55
share ~ pbc(Post.Month, control = pbc.control(inter = 5))
Df AIC
+ Category 2.0001 4069.6
+ Type 2.0000 4081.0
+ Paid 1.0000 4085.5
+ pbc(Post.Weekday) 1.0000 4088.3
+ pbc(Post.Hour) 1.0000 4089.3
<none> 4089.5
- pbc(Post.Month, control = pbc.control(inter = 5)) -2.2657 4113.8
Step: AIC= 4069.59
share ~ pbc(Post.Month, control = pbc.control(inter = 5)) + Category
Df AIC
+ Type 1.99999 4061.9
<none> 4069.6
+ pbc(Post.Hour) 1.00002 4070.1
+ pbc(Post.Weekday) 1.00000 4070.6
+ Paid 0.99994 4072.0
- Category 2.00008 4089.5
- pbc(Post.Month, control = pbc.control(inter = 5)) 1.00010 4090.7
Step: AIC= 4061.92
share ~ pbc(Post.Month, control = pbc.control(inter = 5)) + Category +
Type
Df AIC
+ pbc(Post.Weekday) 0.99998 4058.8
+ pbc(Post.Hour) 1.00010 4060.3
<none> 4061.9
+ Paid 0.99995 4064.9
- Type 1.99999 4069.6
- Category 2.00004 4081.0
- pbc(Post.Month, control = pbc.control(inter = 5)) 1.00010 4085.9
Step: AIC= 4058.83
share ~ pbc(Post.Month, control = pbc.control(inter = 5)) + Category +
Type + pbc(Post.Weekday)
Df AIC
+ pbc(Post.Hour) 1.00008 4058.3
<none> 4058.8
- pbc(Post.Weekday) 0.99998 4061.9
+ Paid 0.99997 4066.3
- Category 2.00000 4069.0
- Type 1.99997 4070.6
- pbc(Post.Month, control = pbc.control(inter = 5)) 1.00008 4082.3
Step: AIC= 4058.34
share ~ pbc(Post.Month, control = pbc.control(inter = 5)) + Category +
Type + pbc(Post.Weekday) + pbc(Post.Hour)
Df AIC
<none> 4058.3
- pbc(Post.Hour) 1.00008 4058.8
- pbc(Post.Weekday) 0.99996 4060.3
+ Paid 0.99993 4066.3
- Category 2.00005 4069.3
- pbc(Post.Month, control = pbc.control(inter = 5)) 1.00005 4070.3
- Type 2.00003 4071.3Final SICHEL model
summary(m.SICHEL)******************************************************************
Family: c("SICHEL", "Sichel")
Call: gamlss(formula = share ~ Category + pbc(Post.Weekday) +
pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour) + Type, sigma.formula = ~Category +
pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour) + pbc(Post.Weekday), nu.formula = ~pbc(Post.Month,
control = pbc.control(inter = 5)) + Category +
Type + pbc(Post.Weekday) + pbc(Post.Hour), family = SICHEL,
data = fbdata, method = mixed(20, 100), trace = FALSE)
Fitting method: mixed(20, 100)
------------------------------------------------------------------
Mu link function: log
Mu Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.85863 0.19238 14.860 < 2e-16 ***
Category2 0.37931 0.10547 3.597 0.000356 ***
Category3 0.52690 0.09557 5.513 5.8e-08 ***
TypePhoto/Video 0.29027 0.19541 1.485 0.138094
TypeStatus 0.63849 0.22728 2.809 0.005172 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.9660 0.2794 7.037 6.96e-12 ***
Category2 -0.3813 0.4483 -0.850 0.39555
Category3 -1.1623 0.4073 -2.854 0.00451 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Nu link function: identity
Nu Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.4902 0.3444 4.327 1.85e-05 ***
Category2 -3.6145 0.3292 -10.981 < 2e-16 ***
Category3 -3.1493 0.2565 -12.280 < 2e-16 ***
TypePhoto/Video -1.3031 0.3560 -3.660 0.00028 ***
TypeStatus 0.5194 0.5144 1.010 0.31321
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
NOTE: Additive smoothing terms exist in the formulas:
i) Std. Error for smoothers are for the linear effect only.
ii) Std. Error for the linear terms maybe are not accurate.
------------------------------------------------------------------
No. of observations in the fit: 495
Degrees of Freedom for the fit: 22.00045
Residual Deg. of Freedom: 472.9996
at cycle: 9
Global Deviance: 4014.34
AIC: 4058.341
SBC: 4150.843
******************************************************************Figure 10.3
Facebook data: Worm plot, Sichel response distribution model (10.1). Twenty realizations of randomized quantile residuals are shown.
rqres.plot(m.SICHEL, howmany=20, plot.type="all", ylim=c(-1.5,1.5))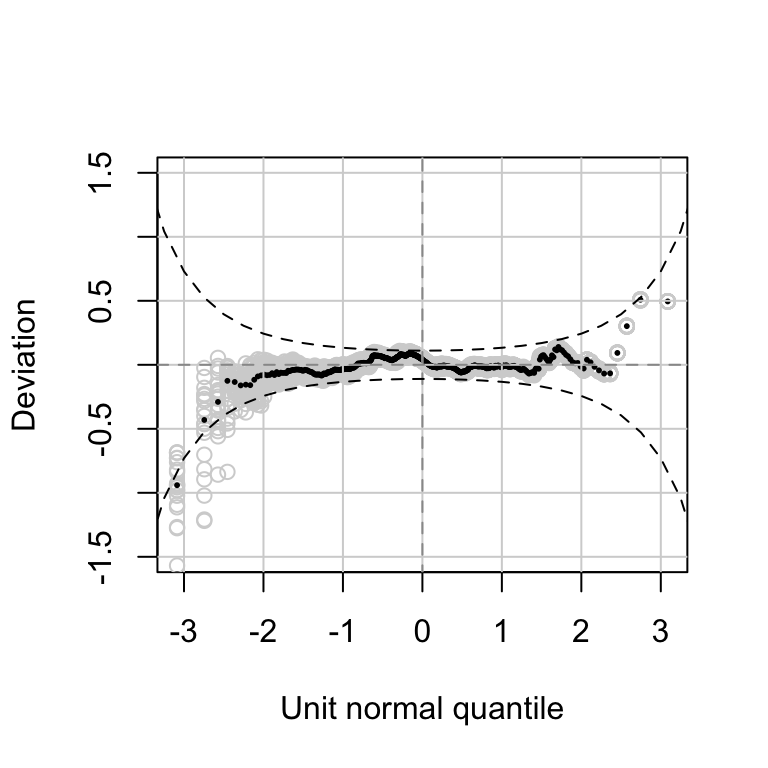
Table 10.2: Prediction scores
The prediction scores in Table 10.2 (MSEP, LS, CRPS, MAPE) are all based on \(K\)-fold cross-validation. The random number generation for obtaining the folds is platform-dependent, so the reader may get results which are numerically slightly different to those obtained here (and reported in Table 10.2).
Alternative models
Neural network: m.NN
# predictors are standardized for more stable results and faster convergence in nn():
fbdata <- mutate(fbdata,
type3 = as.numeric(Type),
Category.s = as.numeric(Category)/3,
Post.Weekday.s = Post.Weekday/7,
Post.Month.s = Post.Month/12,
Post.Hour.s = Post.Hour/24,
type3.s = type3/3)
set.seed(1494)
m.NN <- gamlss(share ~ nn(~ Category.s + Post.Weekday.s + Post.Month.s +
Post.Hour.s + type3, size=3, decay=0.1),
sigma.formula = ~ nn(~ Category.s + Post.Weekday.s + Post.Month.s +
Post.Hour.s + type3, size=3, decay=0.1),
nu.formula = nn(~Category.s + Post.Weekday.s + Post.Month.s +
Post.Hour.s + type3, size=3, decay=0.1),
family = SICHEL, data = fbdata, n.cyc=100)Boosting: m.boost
m.boost <- gamboostLSS(share ~ bols(Category) + bbs(Post.Weekday) + bbs(Post.Month) +
bbs(Post.Hour) + bols(Type),
data = fbdata,
families = as.families("SICHEL"),
method = "noncyclic",
control = boost_control(nu = 0.1))Functions for computing the prediction scores
kfold <- function(data, K, seed=2346){
## sets up vector of indices for K-fold cross-validation
set.seed(seed)
n <- nrow(data)
m <- floor(n/K)
rem <- n%%K
data$row <- 1:n
CV <- data.frame(y=data$share, pred=NA)
I <- sample(c(rep(1:K, each=m), sample(K, rem)))
return(I)
}
kCV <- function(model, data, K, seed=123)
{
## produces model predictions using K-fold cross-validation
data$row <- 1:nrow(data)
CV <- data.frame(y=model$y, pred=NA)
I <- kfold(data, K, seed) # vector of indices for K folds
for(k in 1:K)
{
Itrain <- I!=k
training.data <- data[Itrain,]
testdata <- data[!Itrain,]
mtrain <- update(model, data=training.data)
CV$pred[testdata$row] <- predict(mtrain, newdata=testdata, type="response", data=training.data)
}
return(CV)
}
kCV.boost <- function(model, data, K, seed=123)
{
## produces model predictions using K-fold cross-validation
data$row <- 1:nrow(data)
CV <- data.frame(y=model$mu$response, pred=NA)
I <- kfold(data, K, seed) # vector of indices for K folds
for(k in 1:K)
{
Itrain <- I!=k
training.data <- data[Itrain,]
testdata <- data[!Itrain,]
## The boosting model m.boost has to be hard-coded as it is not
## possible for the update() function to work for boosting
mtrain <- gamboostLSS(share ~ bols(Category) + bbs(Post.Weekday) + bbs(Post.Month) +
bbs(Post.Hour) + bols(Type),
data = training.data,
families = as.families("SICHEL"), method = "noncyclic",
control = boost_control(nu = 0.1))
cvr <- cvrisk(mtrain, grid = 1:200)
mstop(mtrain) <- mstop(cvr)
CV$pred[testdata$row] <- predict(mtrain, newdata=testdata, parameter="mu", type="response",
data=training.data)
}
return(CV)
}Evaluation of MAPE and MSEP for model m.SICHEL:
kfold.gamlss <- kCV(model=m.SICHEL, data=fbdata, K=10, seed=2345)MAPE <- median(100*abs((kfold.gamlss$pred-kfold.gamlss$y)/(kfold.gamlss$y+1)))
MSEP <- mean((kfold.gamlss$pred-kfold.gamlss$y)^2)
MAPE[1] 59.66588MSEP[1] 1810.404Evaluation of MAPE and MSEP for model m.boost:
kfold.boost <- kCV.boost(model=m.boost, data=fbdata, K=10, seed=2345)Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 755.4278
[ 41] ........................................ -- risk: 750.9814
[ 81] ........................................ -- risk: 751.6011
[ 121] ........................................ -- risk: 753.4835
[ 161] .......................................
Final risk: 756.1434
[Fold: 2]
[ 1] ........................................ -- risk: 715.9953
[ 41] ........................................ -- risk: 713.1256
[ 81] ........................................ -- risk: 715.5227
[ 121] ........................................ -- risk: 719.9808
[ 161] .......................................
Final risk: 724.3541
[Fold: 3]
[ 1] ........................................ -- risk: 702.2851
[ 41] ........................................ -- risk: 695.615
[ 81] ........................................ -- risk: 692.6426
[ 121] ........................................ -- risk: 690.814
[ 161] .......................................
Final risk: 689.615
[Fold: 4]
[ 1] ........................................ -- risk: 640.233
[ 41] ........................................ -- risk: 637.5958
[ 81] ........................................ -- risk: 636.4886
[ 121] ........................................ -- risk: 635.2669
[ 161] .......................................
Final risk: 634.7186
[Fold: 5]
[ 1] ........................................ -- risk: 680.5945
[ 41] ........................................ -- risk: 675.1047
[ 81] ........................................ -- risk: 672.9088
[ 121] ........................................ -- risk: 671.6807
[ 161] .......................................
Final risk: 671.15
[Fold: 6]
[ 1] ........................................ -- risk: 674.8549
[ 41] ........................................ -- risk: 668.6113
[ 81] ........................................ -- risk: 666.1524
[ 121] ........................................ -- risk: 664.5611
[ 161] .......................................
Final risk: 663.4622
[Fold: 7]
[ 1] ........................................ -- risk: 748.2578
[ 41] ........................................ -- risk: 742.7342
[ 81] ........................................ -- risk: 740.9662
[ 121] ........................................ -- risk: 740.1988
[ 161] .......................................
Final risk: 740.313
[Fold: 8]
[ 1] ........................................ -- risk: 649.6229
[ 41] ........................................ -- risk: 643.9661
[ 81] ........................................ -- risk: 641.4886
[ 121] ........................................ -- risk: 640.5987
[ 161] .......................................
Final risk: 640.0922
[Fold: 9]
[ 1] ........................................ -- risk: 630.7157
[ 41] ........................................ -- risk: 629.175
[ 81] ........................................ -- risk: 631.8161
[ 121] ........................................ -- risk: 634.4878
[ 161] .......................................
Final risk: 637.5969
[Fold: 10]
[ 1] ........................................ -- risk: 724.2206
[ 41] ........................................ -- risk: 725.157
[ 81] ........................................ -- risk: 729.633
[ 121] ........................................ -- risk: 733.894
[ 161] .......................................
Final risk: 739.3334
[Fold: 11]
[ 1] ........................................ -- risk: 692.7954
[ 41] ........................................ -- risk: 686.6445
[ 81] ........................................ -- risk: 683.9306
[ 121] ........................................ -- risk: 682.4591
[ 161] .......................................
Final risk: 681.6478
[Fold: 12]
[ 1] ........................................ -- risk: 665.6478
[ 41] ........................................ -- risk: 660.3035
[ 81] ........................................ -- risk: 657.4734
[ 121] ........................................ -- risk: 655.776
[ 161] .......................................
Final risk: 654.59
[Fold: 13]
[ 1] ........................................ -- risk: 684.4823
[ 41] ........................................ -- risk: 681.1498
[ 81] ........................................ -- risk: 680.7461
[ 121] ........................................ -- risk: 679.6582
[ 161] .......................................
Final risk: 678.7296
[Fold: 14]
[ 1] ........................................ -- risk: 689.9523
[ 41] ........................................ -- risk: 685.5049
[ 81] ........................................ -- risk: 683.5964
[ 121] ........................................ -- risk: 683.0439
[ 161] .......................................
Final risk: 683.4836
[Fold: 15]
[ 1] ........................................ -- risk: 662.4026
[ 41] ........................................ -- risk: 657.3456
[ 81] ........................................ -- risk: 655.0099
[ 121] ........................................ -- risk: 653.6937
[ 161] .......................................
Final risk: 652.7089
[Fold: 16]
[ 1] ........................................ -- risk: 702.4429
[ 41] ........................................ -- risk: 699.2617
[ 81] ........................................ -- risk: 700.0087
[ 121] ........................................ -- risk: 701.465
[ 161] .......................................
Final risk: 703.7386
[Fold: 17]
[ 1] ........................................ -- risk: 671.3921
[ 41] ........................................ -- risk: 665.2957
[ 81] ........................................ -- risk: 662.556
[ 121] ........................................ -- risk: 660.9186
[ 161] .......................................
Final risk: 659.5653
[Fold: 18]
[ 1] ........................................ -- risk: 673.576
[ 41] ........................................ -- risk: 670.5247
[ 81] ........................................ -- risk: 669.7006
[ 121] ........................................ -- risk: 669.5206
[ 161] .......................................
Final risk: 669.6411
[Fold: 19]
[ 1] ........................................ -- risk: 732.1677
[ 41] ........................................ -- risk: 729.5639
[ 81] ........................................ -- risk: 732.3215
[ 121] ........................................ -- risk: 737.9805
[ 161] .......................................
Final risk: 743.8184
[Fold: 20]
[ 1] ........................................ -- risk: 710.3143
[ 41] ........................................ -- risk: 703.3932
[ 81] ........................................ -- risk: 700.8107
[ 121] ........................................ -- risk: 699.9733
[ 161] .......................................
Final risk: 699.8748
[Fold: 21]
[ 1] ........................................ -- risk: 697.4509
[ 41] ........................................ -- risk: 693.7002
[ 81] ........................................ -- risk: 695.0853
[ 121] ........................................ -- risk: 696.9809
[ 161] .......................................
Final risk: 699.4606
[Fold: 22]
[ 1] ........................................ -- risk: 739.3979
[ 41] ........................................ -- risk: 736.7783
[ 81] ........................................ -- risk: 739.2467
[ 121] ........................................ -- risk: 743.0699
[ 161] .......................................
Final risk: 747.585
[Fold: 23]
[ 1] ........................................ -- risk: 702.1993
[ 41] ........................................ -- risk: 698.9396
[ 81] ........................................ -- risk: 700.7171
[ 121] ........................................ -- risk: 703.8816
[ 161] .......................................
Final risk: 707.7119
[Fold: 24]
[ 1] ........................................ -- risk: 669.2894
[ 41] ........................................ -- risk: 665.8495
[ 81] ........................................ -- risk: 665.3928
[ 121] ........................................ -- risk: 666.6779
[ 161] .......................................
Final risk: 669.1326
[Fold: 25]
[ 1] ........................................ -- risk: 730.0618
[ 41] ........................................ -- risk: 727.2817
[ 81] ........................................ -- risk: 726.8666
[ 121] ........................................ -- risk: 726.9869
[ 161] .......................................
Final risk: 727.7268
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 738.1169
[ 41] ........................................ -- risk: 733.3154
[ 81] ........................................ -- risk: 731.2009
[ 121] ........................................ -- risk: 730.493
[ 161] .......................................
Final risk: 730.3066
[Fold: 2]
[ 1] ........................................ -- risk: 700.4371
[ 41] ........................................ -- risk: 697.1746
[ 81] ........................................ -- risk: 699.1511
[ 121] ........................................ -- risk: 702.2957
[ 161] .......................................
Final risk: 705.8679
[Fold: 3]
[ 1] ........................................ -- risk: 706.105
[ 41] ........................................ -- risk: 701.2745
[ 81] ........................................ -- risk: 699.0671
[ 121] ........................................ -- risk: 697.8085
[ 161] .......................................
Final risk: 697.6171
[Fold: 4]
[ 1] ........................................ -- risk: 660.538
[ 41] ........................................ -- risk: 655.0052
[ 81] ........................................ -- risk: 651.6999
[ 121] ........................................ -- risk: 649.9377
[ 161] .......................................
Final risk: 649.0897
[Fold: 5]
[ 1] ........................................ -- risk: 691.6674
[ 41] ........................................ -- risk: 688.6865
[ 81] ........................................ -- risk: 686.1831
[ 121] ........................................ -- risk: 684.6837
[ 161] .......................................
Final risk: 684.0967
[Fold: 6]
[ 1] ........................................ -- risk: 658.7214
[ 41] ........................................ -- risk: 653.1354
[ 81] ........................................ -- risk: 651.5394
[ 121] ........................................ -- risk: 651.0042
[ 161] .......................................
Final risk: 651.0385
[Fold: 7]
[ 1] ........................................ -- risk: 722.0167
[ 41] ........................................ -- risk: 717.3777
[ 81] ........................................ -- risk: 715.8945
[ 121] ........................................ -- risk: 715.7953
[ 161] .......................................
Final risk: 716.1516
[Fold: 8]
[ 1] ........................................ -- risk: 709.395
[ 41] ........................................ -- risk: 702.3443
[ 81] ........................................ -- risk: 698.6983
[ 121] ........................................ -- risk: 696.8134
[ 161] .......................................
Final risk: 695.6362
[Fold: 9]
[ 1] ........................................ -- risk: 737.6502
[ 41] ........................................ -- risk: 737.565
[ 81] ........................................ -- risk: 742.308
[ 121] ........................................ -- risk: 749.3168
[ 161] .......................................
Final risk: 755.4067
[Fold: 10]
[ 1] ........................................ -- risk: 733.8546
[ 41] ........................................ -- risk: 729.0285
[ 81] ........................................ -- risk: 727.8121
[ 121] ........................................ -- risk: 728.7358
[ 161] .......................................
Final risk: 731.0487
[Fold: 11]
[ 1] ........................................ -- risk: 656.7613
[ 41] ........................................ -- risk: 652.08
[ 81] ........................................ -- risk: 650.8459
[ 121] ........................................ -- risk: 650.5637
[ 161] .......................................
Final risk: 650.1647
[Fold: 12]
[ 1] ........................................ -- risk: 734.2592
[ 41] ........................................ -- risk: 729.5376
[ 81] ........................................ -- risk: 726.651
[ 121] ........................................ -- risk: 724.9237
[ 161] .......................................
Final risk: 724.4093
[Fold: 13]
[ 1] ........................................ -- risk: 682.7848
[ 41] ........................................ -- risk: 679.8545
[ 81] ........................................ -- risk: 679.0432
[ 121] ........................................ -- risk: 679.1269
[ 161] .......................................
Final risk: 679.045
[Fold: 14]
[ 1] ........................................ -- risk: 729.7233
[ 41] ........................................ -- risk: 731.2937
[ 81] ........................................ -- risk: 735.1928
[ 121] ........................................ -- risk: 738.6134
[ 161] .......................................
Final risk: 743.252
[Fold: 15]
[ 1] ........................................ -- risk: 705.1063
[ 41] ........................................ -- risk: 701.4521
[ 81] ........................................ -- risk: 700.7174
[ 121] ........................................ -- risk: 701.3897
[ 161] .......................................
Final risk: 702.3831
[Fold: 16]
[ 1] ........................................ -- risk: 673.7552
[ 41] ........................................ -- risk: 670.6491
[ 81] ........................................ -- risk: 669.1164
[ 121] ........................................ -- risk: 668.7832
[ 161] .......................................
Final risk: 668.4176
[Fold: 17]
[ 1] ........................................ -- risk: 663.8819
[ 41] ........................................ -- risk: 658.1433
[ 81] ........................................ -- risk: 655.5179
[ 121] ........................................ -- risk: 654.0635
[ 161] .......................................
Final risk: 653.3462
[Fold: 18]
[ 1] ........................................ -- risk: 699.6181
[ 41] ........................................ -- risk: 691.8037
[ 81] ........................................ -- risk: 688.7335
[ 121] ........................................ -- risk: 687.076
[ 161] .......................................
Final risk: 686.0339
[Fold: 19]
[ 1] ........................................ -- risk: 693.2098
[ 41] ........................................ -- risk: 689.8525
[ 81] ........................................ -- risk: 687.9717
[ 121] ........................................ -- risk: 687.2719
[ 161] .......................................
Final risk: 686.4905
[Fold: 20]
[ 1] ........................................ -- risk: 707.1054
[ 41] ........................................ -- risk: 701.3298
[ 81] ........................................ -- risk: 698.4025
[ 121] ........................................ -- risk: 696.7888
[ 161] .......................................
Final risk: 696.1466
[Fold: 21]
[ 1] ........................................ -- risk: 700.3705
[ 41] ........................................ -- risk: 699.872
[ 81] ........................................ -- risk: 702.5468
[ 121] ........................................ -- risk: 706.0323
[ 161] .......................................
Final risk: 709.8274
[Fold: 22]
[ 1] ........................................ -- risk: 764.238
[ 41] ........................................ -- risk: 762.0417
[ 81] ........................................ -- risk: 765.7709
[ 121] ........................................ -- risk: 771.0044
[ 161] .......................................
Final risk: 776.9657
[Fold: 23]
[ 1] ........................................ -- risk: 649.7864
[ 41] ........................................ -- risk: 642.141
[ 81] ........................................ -- risk: 638.4208
[ 121] ........................................ -- risk: 635.8657
[ 161] .......................................
Final risk: 634.3165
[Fold: 24]
[ 1] ........................................ -- risk: 696.6859
[ 41] ........................................ -- risk: 693.0261
[ 81] ........................................ -- risk: 692.6888
[ 121] ........................................ -- risk: 692.7721
[ 161] .......................................
Final risk: 694.3049
[Fold: 25]
[ 1] ........................................ -- risk: 697.5446
[ 41] ........................................ -- risk: 692.5444
[ 81] ........................................ -- risk: 692.4405
[ 121] ........................................ -- risk: 693.9504
[ 161] .......................................
Final risk: 696.3383
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 685.9959
[ 41] ........................................ -- risk: 683.5098
[ 81] ........................................ -- risk: 682.5302
[ 121] ........................................ -- risk: 682.3073
[ 161] .......................................
Final risk: 683.1187
[Fold: 2]
[ 1] ........................................ -- risk: 692.4701
[ 41] ........................................ -- risk: 693.6247
[ 81] ........................................ -- risk: 698.4621
[ 121] ........................................ -- risk: 702.5647
[ 161] .......................................
Final risk: 707.7482
[Fold: 3]
[ 1] ........................................ -- risk: 719.3278
[ 41] ........................................ -- risk: 715.1009
[ 81] ........................................ -- risk: 714.386
[ 121] ........................................ -- risk: 715.2136
[ 161] .......................................
Final risk: 717.6971
[Fold: 4]
[ 1] ........................................ -- risk: 666.0248
[ 41] ........................................ -- risk: 664.4393
[ 81] ........................................ -- risk: 665.222
[ 121] ........................................ -- risk: 665.6298
[ 161] .......................................
Final risk: 666.1362
[Fold: 5]
[ 1] ........................................ -- risk: 695.7425
[ 41] ........................................ -- risk: 695.3592
[ 81] ........................................ -- risk: 697.9689
[ 121] ........................................ -- risk: 701.3943
[ 161] .......................................
Final risk: 703.969
[Fold: 6]
[ 1] ........................................ -- risk: 715.4008
[ 41] ........................................ -- risk: 711.8849
[ 81] ........................................ -- risk: 712.4655
[ 121] ........................................ -- risk: 714.1292
[ 161] .......................................
Final risk: 716.687
[Fold: 7]
[ 1] ........................................ -- risk: 659.8137
[ 41] ........................................ -- risk: 654.3526
[ 81] ........................................ -- risk: 651.6833
[ 121] ........................................ -- risk: 650.1947
[ 161] .......................................
Final risk: 649.5394
[Fold: 8]
[ 1] ........................................ -- risk: 658.2622
[ 41] ........................................ -- risk: 652.4282
[ 81] ........................................ -- risk: 649.8294
[ 121] ........................................ -- risk: 648.6278
[ 161] .......................................
Final risk: 648.5079
[Fold: 9]
[ 1] ........................................ -- risk: 706.9807
[ 41] ........................................ -- risk: 703.8062
[ 81] ........................................ -- risk: 702.178
[ 121] ........................................ -- risk: 700.6313
[ 161] .......................................
Final risk: 699.9039
[Fold: 10]
[ 1] ........................................ -- risk: 673.3163
[ 41] ........................................ -- risk: 670.472
[ 81] ........................................ -- risk: 669.3928
[ 121] ........................................ -- risk: 667.7579
[ 161] .......................................
Final risk: 666.8205
[Fold: 11]
[ 1] ........................................ -- risk: 681.3287
[ 41] ........................................ -- risk: 677.9966
[ 81] ........................................ -- risk: 675.8816
[ 121] ........................................ -- risk: 673.8147
[ 161] .......................................
Final risk: 672.5642
[Fold: 12]
[ 1] ........................................ -- risk: 671.3459
[ 41] ........................................ -- risk: 668.5488
[ 81] ........................................ -- risk: 666.6829
[ 121] ........................................ -- risk: 666.1846
[ 161] .......................................
Final risk: 666.4717
[Fold: 13]
[ 1] ........................................ -- risk: 649.7356
[ 41] ........................................ -- risk: 646.5451
[ 81] ........................................ -- risk: 643.8166
[ 121] ........................................ -- risk: 641.0582
[ 161] .......................................
Final risk: 639.0088
[Fold: 14]
[ 1] ........................................ -- risk: 637.7752
[ 41] ........................................ -- risk: 635.6802
[ 81] ........................................ -- risk: 634.8883
[ 121] ........................................ -- risk: 634.8089
[ 161] .......................................
Final risk: 634.7599
[Fold: 15]
[ 1] ........................................ -- risk: 688.2219
[ 41] ........................................ -- risk: 683.0469
[ 81] ........................................ -- risk: 680.5363
[ 121] ........................................ -- risk: 679.32
[ 161] .......................................
Final risk: 678.1057
[Fold: 16]
[ 1] ........................................ -- risk: 681.5742
[ 41] ........................................ -- risk: 676.9715
[ 81] ........................................ -- risk: 673.7247
[ 121] ........................................ -- risk: 671.6737
[ 161] .......................................
Final risk: 670.767
[Fold: 17]
[ 1] ........................................ -- risk: 703.3602
[ 41] ........................................ -- risk: 697.6868
[ 81] ........................................ -- risk: 694.954
[ 121] ........................................ -- risk: 693.2953
[ 161] .......................................
Final risk: 692.3019
[Fold: 18]
[ 1] ........................................ -- risk: 707.4339
[ 41] ........................................ -- risk: 704.3544
[ 81] ........................................ -- risk: 703.3045
[ 121] ........................................ -- risk: 703.0338
[ 161] .......................................
Final risk: 702.4143
[Fold: 19]
[ 1] ........................................ -- risk: 688.3896
[ 41] ........................................ -- risk: 684.0242
[ 81] ........................................ -- risk: 682.2065
[ 121] ........................................ -- risk: 681.3935
[ 161] .......................................
Final risk: 681.6633
[Fold: 20]
[ 1] ........................................ -- risk: 740.3701
[ 41] ........................................ -- risk: 738.4104
[ 81] ........................................ -- risk: 737.6042
[ 121] ........................................ -- risk: 738.6823
[ 161] .......................................
Final risk: 740.2645
[Fold: 21]
[ 1] ........................................ -- risk: 681.2687
[ 41] ........................................ -- risk: 678.8415
[ 81] ........................................ -- risk: 679.4382
[ 121] ........................................ -- risk: 681.496
[ 161] .......................................
Final risk: 684.4506
[Fold: 22]
[ 1] ........................................ -- risk: 660.454
[ 41] ........................................ -- risk: 657.6336
[ 81] ........................................ -- risk: 656.3682
[ 121] ........................................ -- risk: 655.8296
[ 161] .......................................
Final risk: 656.3259
[Fold: 23]
[ 1] ........................................ -- risk: 709.7149
[ 41] ........................................ -- risk: 708.0398
[ 81] ........................................ -- risk: 709.214
[ 121] ........................................ -- risk: 710.9574
[ 161] .......................................
Final risk: 713.3839
[Fold: 24]
[ 1] ........................................ -- risk: 648.6612
[ 41] ........................................ -- risk: 646.3673
[ 81] ........................................ -- risk: 644.4267
[ 121] ........................................ -- risk: 642.8724
[ 161] .......................................
Final risk: 641.913
[Fold: 25]
[ 1] ........................................ -- risk: 688.7726
[ 41] ........................................ -- risk: 685.2963
[ 81] ........................................ -- risk: 685.7472
[ 121] ........................................ -- risk: 687.296
[ 161] .......................................
Final risk: 689.1697
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 672.9057
[ 41] ........................................ -- risk: 669.4112
[ 81] ........................................ -- risk: 667.8702
[ 121] ........................................ -- risk: 667.3426
[ 161] .......................................
Final risk: 667.1883
[Fold: 2]
[ 1] ........................................ -- risk: 667.7363
[ 41] ........................................ -- risk: 666.1606
[ 81] ........................................ -- risk: 664.3035
[ 121] ........................................ -- risk: 662.5101
[ 161] .......................................
Final risk: 661.572
[Fold: 3]
[ 1] ........................................ -- risk: 702.5493
[ 41] ........................................ -- risk: 696.2071
[ 81] ........................................ -- risk: 693.5018
[ 121] ........................................ -- risk: 692.4873
[ 161] .......................................
Final risk: 692.1039
[Fold: 4]
[ 1] ........................................ -- risk: 736.1536
[ 41] ........................................ -- risk: 729.3601
[ 81] ........................................ -- risk: 726.7622
[ 121] ........................................ -- risk: 725.3138
[ 161] .......................................
Final risk: 724.8837
[Fold: 5]
[ 1] ........................................ -- risk: 692.218
[ 41] ........................................ -- risk: 686.4048
[ 81] ........................................ -- risk: 683.9372
[ 121] ........................................ -- risk: 682.5743
[ 161] .......................................
Final risk: 682.0197
[Fold: 6]
[ 1] ........................................ -- risk: 684.5882
[ 41] ........................................ -- risk: 686.1024
[ 81] ........................................ -- risk: 690.8617
[ 121] ........................................ -- risk: 696.4134
[ 161] .......................................
Final risk: 701.9678
[Fold: 7]
[ 1] ........................................ -- risk: 702.1734
[ 41] ........................................ -- risk: 699.5134
[ 81] ........................................ -- risk: 698.2821
[ 121] ........................................ -- risk: 698.0935
[ 161] .......................................
Final risk: 698.2925
[Fold: 8]
[ 1] ........................................ -- risk: 703.5914
[ 41] ........................................ -- risk: 699.4699
[ 81] ........................................ -- risk: 697.2677
[ 121] ........................................ -- risk: 696.2297
[ 161] .......................................
Final risk: 696.0589
[Fold: 9]
[ 1] ........................................ -- risk: 670.6997
[ 41] ........................................ -- risk: 672.6566
[ 81] ........................................ -- risk: 678.8042
[ 121] ........................................ -- risk: 687.079
[ 161] .......................................
Final risk: 695.684
[Fold: 10]
[ 1] ........................................ -- risk: 670.9862
[ 41] ........................................ -- risk: 669.3894
[ 81] ........................................ -- risk: 672.5947
[ 121] ........................................ -- risk: 676.3489
[ 161] .......................................
Final risk: 679.7663
[Fold: 11]
[ 1] ........................................ -- risk: 620.5791
[ 41] ........................................ -- risk: 618.5803
[ 81] ........................................ -- risk: 615.9579
[ 121] ........................................ -- risk: 614.2622
[ 161] .......................................
Final risk: 613.0813
[Fold: 12]
[ 1] ........................................ -- risk: 734.0861
[ 41] ........................................ -- risk: 729.0017
[ 81] ........................................ -- risk: 726.8331
[ 121] ........................................ -- risk: 726.2675
[ 161] .......................................
Final risk: 726.8851
[Fold: 13]
[ 1] ........................................ -- risk: 672.4761
[ 41] ........................................ -- risk: 667.2185
[ 81] ........................................ -- risk: 664.7455
[ 121] ........................................ -- risk: 663.4808
[ 161] .......................................
Final risk: 662.6158
[Fold: 14]
[ 1] ........................................ -- risk: 690.685
[ 41] ........................................ -- risk: 687.6228
[ 81] ........................................ -- risk: 685.0981
[ 121] ........................................ -- risk: 683.2942
[ 161] .......................................
Final risk: 682.1378
[Fold: 15]
[ 1] ........................................ -- risk: 631.1374
[ 41] ........................................ -- risk: 628.7229
[ 81] ........................................ -- risk: 627.4747
[ 121] ........................................ -- risk: 626.4517
[ 161] .......................................
Final risk: 626.058
[Fold: 16]
[ 1] ........................................ -- risk: 698.4469
[ 41] ........................................ -- risk: 696.2081
[ 81] ........................................ -- risk: 695.3167
[ 121] ........................................ -- risk: 695.1934
[ 161] .......................................
Final risk: 695.9542
[Fold: 17]
[ 1] ........................................ -- risk: 700.6937
[ 41] ........................................ -- risk: 700.6829
[ 81] ........................................ -- risk: 703.9378
[ 121] ........................................ -- risk: 708.7294
[ 161] .......................................
Final risk: 713.8679
[Fold: 18]
[ 1] ........................................ -- risk: 696.6891
[ 41] ........................................ -- risk: 692.3035
[ 81] ........................................ -- risk: 690.4937
[ 121] ........................................ -- risk: 689.3489
[ 161] .......................................
Final risk: 689.281
[Fold: 19]
[ 1] ........................................ -- risk: 727.7272
[ 41] ........................................ -- risk: 724.1878
[ 81] ........................................ -- risk: 723.8481
[ 121] ........................................ -- risk: 723.4908
[ 161] .......................................
Final risk: 723.3519
[Fold: 20]
[ 1] ........................................ -- risk: 703.4112
[ 41] ........................................ -- risk: 701.0352
[ 81] ........................................ -- risk: 698.8999
[ 121] ........................................ -- risk: 697.0547
[ 161] .......................................
Final risk: 695.9412
[Fold: 21]
[ 1] ........................................ -- risk: 684.5831
[ 41] ........................................ -- risk: 679.628
[ 81] ........................................ -- risk: 677.0714
[ 121] ........................................ -- risk: 675.7619
[ 161] .......................................
Final risk: 674.9743
[Fold: 22]
[ 1] ........................................ -- risk: 698.3931
[ 41] ........................................ -- risk: 697.424
[ 81] ........................................ -- risk: 700.0726
[ 121] ........................................ -- risk: 703.6996
[ 161] .......................................
Final risk: 706.0794
[Fold: 23]
[ 1] ........................................ -- risk: 679.9917
[ 41] ........................................ -- risk: 677.1728
[ 81] ........................................ -- risk: 677.9409
[ 121] ........................................ -- risk: 679.8617
[ 161] .......................................
Final risk: 681.6704
[Fold: 24]
[ 1] ........................................ -- risk: 718.556
[ 41] ........................................ -- risk: 712.3423
[ 81] ........................................ -- risk: 709.0152
[ 121] ........................................ -- risk: 706.9684
[ 161] .......................................
Final risk: 705.7235
[Fold: 25]
[ 1] ........................................ -- risk: 764.0229
[ 41] ........................................ -- risk: 759.9544
[ 81] ........................................ -- risk: 759.44
[ 121] ........................................ -- risk: 758.6511
[ 161] .......................................
Final risk: 758.871
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 683.4815
[ 41] ........................................ -- risk: 681.7153
[ 81] ........................................ -- risk: 680.2759
[ 121] ........................................ -- risk: 679.874
[ 161] .......................................
Final risk: 680.5982
[Fold: 2]
[ 1] ........................................ -- risk: 679.5348
[ 41] ........................................ -- risk: 672.4967
[ 81] ........................................ -- risk: 669.9691
[ 121] ........................................ -- risk: 667.5027
[ 161] .......................................
Final risk: 665.5317
[Fold: 3]
[ 1] ........................................ -- risk: 642.863
[ 41] ........................................ -- risk: 640.5319
[ 81] ........................................ -- risk: 639.3096
[ 121] ........................................ -- risk: 639.5859
[ 161] .......................................
Final risk: 639.8701
[Fold: 4]
[ 1] ........................................ -- risk: 652.5322
[ 41] ........................................ -- risk: 651.7315
[ 81] ........................................ -- risk: 657.3675
[ 121] ........................................ -- risk: 666.102
[ 161] .......................................
Final risk: 674.344
[Fold: 5]
[ 1] ........................................ -- risk: 676.0397
[ 41] ........................................ -- risk: 673.7042
[ 81] ........................................ -- risk: 678.3512
[ 121] ........................................ -- risk: 686.7972
[ 161] .......................................
Final risk: 695.7122
[Fold: 6]
[ 1] ........................................ -- risk: 633.5209
[ 41] ........................................ -- risk: 631.0058
[ 81] ........................................ -- risk: 630.2585
[ 121] ........................................ -- risk: 630.2646
[ 161] .......................................
Final risk: 630.4324
[Fold: 7]
[ 1] ........................................ -- risk: 682.0576
[ 41] ........................................ -- risk: 675.0178
[ 81] ........................................ -- risk: 671.6366
[ 121] ........................................ -- risk: 669.7714
[ 161] .......................................
Final risk: 668.7877
[Fold: 8]
[ 1] ........................................ -- risk: 663.1575
[ 41] ........................................ -- risk: 656.4844
[ 81] ........................................ -- risk: 653.0174
[ 121] ........................................ -- risk: 651.5604
[ 161] .......................................
Final risk: 650.0704
[Fold: 9]
[ 1] ........................................ -- risk: 657.0151
[ 41] ........................................ -- risk: 652.6737
[ 81] ........................................ -- risk: 650.5625
[ 121] ........................................ -- risk: 649.0763
[ 161] .......................................
Final risk: 648.5997
[Fold: 10]
[ 1] ........................................ -- risk: 703.313
[ 41] ........................................ -- risk: 704.0411
[ 81] ........................................ -- risk: 710.1096
[ 121] ........................................ -- risk: 717.7831
[ 161] .......................................
Final risk: 724.5738
[Fold: 11]
[ 1] ........................................ -- risk: 694.2553
[ 41] ........................................ -- risk: 689.3424
[ 81] ........................................ -- risk: 687.1121
[ 121] ........................................ -- risk: 685.853
[ 161] .......................................
Final risk: 685.2625
[Fold: 12]
[ 1] ........................................ -- risk: 722.4253
[ 41] ........................................ -- risk: 717.8926
[ 81] ........................................ -- risk: 716.8954
[ 121] ........................................ -- risk: 717.7808
[ 161] .......................................
Final risk: 719.6808
[Fold: 13]
[ 1] ........................................ -- risk: 714.4131
[ 41] ........................................ -- risk: 707.9109
[ 81] ........................................ -- risk: 705.5307
[ 121] ........................................ -- risk: 704.037
[ 161] .......................................
Final risk: 703.8228
[Fold: 14]
[ 1] ........................................ -- risk: 643.1578
[ 41] ........................................ -- risk: 638.0105
[ 81] ........................................ -- risk: 634.4462
[ 121] ........................................ -- risk: 632.171
[ 161] .......................................
Final risk: 631.5209
[Fold: 15]
[ 1] ........................................ -- risk: 719.4434
[ 41] ........................................ -- risk: 713.1652
[ 81] ........................................ -- risk: 710.6528
[ 121] ........................................ -- risk: 709.7236
[ 161] .......................................
Final risk: 709.4256
[Fold: 16]
[ 1] ........................................ -- risk: 690.1369
[ 41] ........................................ -- risk: 688.8009
[ 81] ........................................ -- risk: 693.8438
[ 121] ........................................ -- risk: 699.653
[ 161] .......................................
Final risk: 703.7696
[Fold: 17]
[ 1] ........................................ -- risk: 694.765
[ 41] ........................................ -- risk: 688.2493
[ 81] ........................................ -- risk: 686.4797
[ 121] ........................................ -- risk: 686.2774
[ 161] .......................................
Final risk: 687.137
[Fold: 18]
[ 1] ........................................ -- risk: 688.6114
[ 41] ........................................ -- risk: 680.6311
[ 81] ........................................ -- risk: 677.2536
[ 121] ........................................ -- risk: 674.9261
[ 161] .......................................
Final risk: 673.5749
[Fold: 19]
[ 1] ........................................ -- risk: 757.4486
[ 41] ........................................ -- risk: 755.6299
[ 81] ........................................ -- risk: 757.1974
[ 121] ........................................ -- risk: 762.2113
[ 161] .......................................
Final risk: 767.5112
[Fold: 20]
[ 1] ........................................ -- risk: 768.5773
[ 41] ........................................ -- risk: 769.6435
[ 81] ........................................ -- risk: 774.3978
[ 121] ........................................ -- risk: 780.1762
[ 161] .......................................
Final risk: 785.7156
[Fold: 21]
[ 1] ........................................ -- risk: 733.7569
[ 41] ........................................ -- risk: 728.1455
[ 81] ........................................ -- risk: 728.3788
[ 121] ........................................ -- risk: 729.4903
[ 161] .......................................
Final risk: 730.049
[Fold: 22]
[ 1] ........................................ -- risk: 707.5097
[ 41] ........................................ -- risk: 703.2092
[ 81] ........................................ -- risk: 702.2991
[ 121] ........................................ -- risk: 701.3881
[ 161] .......................................
Final risk: 700.7526
[Fold: 23]
[ 1] ........................................ -- risk: 719.3558
[ 41] ........................................ -- risk: 715.4671
[ 81] ........................................ -- risk: 714.1617
[ 121] ........................................ -- risk: 714.6298
[ 161] .......................................
Final risk: 716.1897
[Fold: 24]
[ 1] ........................................ -- risk: 722.544
[ 41] ........................................ -- risk: 720.2985
[ 81] ........................................ -- risk: 718.4826
[ 121] ........................................ -- risk: 717.2657
[ 161] .......................................
Final risk: 716.7339
[Fold: 25]
[ 1] ........................................ -- risk: 707.8485
[ 41] ........................................ -- risk: 709.4144
[ 81] ........................................ -- risk: 715.1748
[ 121] ........................................ -- risk: 722.2929
[ 161] .......................................
Final risk: 727.5174
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 731.2111
[ 41] ........................................ -- risk: 725.3914
[ 81] ........................................ -- risk: 723.7641
[ 121] ........................................ -- risk: 723.3543
[ 161] .......................................
Final risk: 723.2843
[Fold: 2]
[ 1] ........................................ -- risk: 675.1516
[ 41] ........................................ -- risk: 670.2271
[ 81] ........................................ -- risk: 668.6409
[ 121] ........................................ -- risk: 667.8827
[ 161] .......................................
Final risk: 667.7223
[Fold: 3]
[ 1] ........................................ -- risk: 694.0041
[ 41] ........................................ -- risk: 691.3793
[ 81] ........................................ -- risk: 693.4115
[ 121] ........................................ -- risk: 697.6713
[ 161] .......................................
Final risk: 702.8738
[Fold: 4]
[ 1] ........................................ -- risk: 718.3783
[ 41] ........................................ -- risk: 716.3915
[ 81] ........................................ -- risk: 718.0497
[ 121] ........................................ -- risk: 720.4646
[ 161] .......................................
Final risk: 723.1807
[Fold: 5]
[ 1] ........................................ -- risk: 694.7809
[ 41] ........................................ -- risk: 692.1876
[ 81] ........................................ -- risk: 691.5731
[ 121] ........................................ -- risk: 690.9101
[ 161] .......................................
Final risk: 690.3598
[Fold: 6]
[ 1] ........................................ -- risk: 683.193
[ 41] ........................................ -- risk: 676.4554
[ 81] ........................................ -- risk: 673.96
[ 121] ........................................ -- risk: 672.5197
[ 161] .......................................
Final risk: 671.8933
[Fold: 7]
[ 1] ........................................ -- risk: 718.4372
[ 41] ........................................ -- risk: 711.3052
[ 81] ........................................ -- risk: 708.5204
[ 121] ........................................ -- risk: 707.1211
[ 161] .......................................
Final risk: 706.2523
[Fold: 8]
[ 1] ........................................ -- risk: 711.056
[ 41] ........................................ -- risk: 710.3082
[ 81] ........................................ -- risk: 711.4831
[ 121] ........................................ -- risk: 713.0274
[ 161] .......................................
Final risk: 714.4128
[Fold: 9]
[ 1] ........................................ -- risk: 669.0263
[ 41] ........................................ -- risk: 663.3727
[ 81] ........................................ -- risk: 662.1788
[ 121] ........................................ -- risk: 661.1878
[ 161] .......................................
Final risk: 660.1848
[Fold: 10]
[ 1] ........................................ -- risk: 672.2846
[ 41] ........................................ -- risk: 673.9403
[ 81] ........................................ -- risk: 677.7638
[ 121] ........................................ -- risk: 683.492
[ 161] .......................................
Final risk: 689.565
[Fold: 11]
[ 1] ........................................ -- risk: 680.6403
[ 41] ........................................ -- risk: 677.1597
[ 81] ........................................ -- risk: 675.6791
[ 121] ........................................ -- risk: 674.7424
[ 161] .......................................
Final risk: 674.3914
[Fold: 12]
[ 1] ........................................ -- risk: 728.0993
[ 41] ........................................ -- risk: 723.8851
[ 81] ........................................ -- risk: 722.4859
[ 121] ........................................ -- risk: 722.019
[ 161] .......................................
Final risk: 722.2765
[Fold: 13]
[ 1] ........................................ -- risk: 677.7291
[ 41] ........................................ -- risk: 675.4294
[ 81] ........................................ -- risk: 675.5346
[ 121] ........................................ -- risk: 677.2417
[ 161] .......................................
Final risk: 679.5119
[Fold: 14]
[ 1] ........................................ -- risk: 723.8025
[ 41] ........................................ -- risk: 725.4038
[ 81] ........................................ -- risk: 729.2716
[ 121] ........................................ -- risk: 734.1643
[ 161] .......................................
Final risk: 738.3388
[Fold: 15]
[ 1] ........................................ -- risk: 652.6435
[ 41] ........................................ -- risk: 648.9779
[ 81] ........................................ -- risk: 649.3894
[ 121] ........................................ -- risk: 650.8026
[ 161] .......................................
Final risk: 653.3757
[Fold: 16]
[ 1] ........................................ -- risk: 718.6964
[ 41] ........................................ -- risk: 713.5526
[ 81] ........................................ -- risk: 710.942
[ 121] ........................................ -- risk: 709.2504
[ 161] .......................................
Final risk: 708.396
[Fold: 17]
[ 1] ........................................ -- risk: 652.8077
[ 41] ........................................ -- risk: 646.2576
[ 81] ........................................ -- risk: 643.4316
[ 121] ........................................ -- risk: 642.5444
[ 161] .......................................
Final risk: 641.8173
[Fold: 18]
[ 1] ........................................ -- risk: 717.3282
[ 41] ........................................ -- risk: 717.9709
[ 81] ........................................ -- risk: 723.1336
[ 121] ........................................ -- risk: 727.5876
[ 161] .......................................
Final risk: 732.8775
[Fold: 19]
[ 1] ........................................ -- risk: 710.8589
[ 41] ........................................ -- risk: 703.9751
[ 81] ........................................ -- risk: 701.4418
[ 121] ........................................ -- risk: 700.2762
[ 161] .......................................
Final risk: 699.3325
[Fold: 20]
[ 1] ........................................ -- risk: 728.8644
[ 41] ........................................ -- risk: 725.7576
[ 81] ........................................ -- risk: 724.9065
[ 121] ........................................ -- risk: 725.6736
[ 161] .......................................
Final risk: 726.6799
[Fold: 21]
[ 1] ........................................ -- risk: 685.3667
[ 41] ........................................ -- risk: 683.0732
[ 81] ........................................ -- risk: 682.2232
[ 121] ........................................ -- risk: 681.8767
[ 161] .......................................
Final risk: 681.7447
[Fold: 22]
[ 1] ........................................ -- risk: 723.897
[ 41] ........................................ -- risk: 722.1667
[ 81] ........................................ -- risk: 720.8093
[ 121] ........................................ -- risk: 720.0049
[ 161] .......................................
Final risk: 719.5567
[Fold: 23]
[ 1] ........................................ -- risk: 667.8216
[ 41] ........................................ -- risk: 663.5878
[ 81] ........................................ -- risk: 663.3026
[ 121] ........................................ -- risk: 663.7073
[ 161] .......................................
Final risk: 663.797
[Fold: 24]
[ 1] ........................................ -- risk: 692.1774
[ 41] ........................................ -- risk: 686.8298
[ 81] ........................................ -- risk: 685.8344
[ 121] ........................................ -- risk: 685.4743
[ 161] .......................................
Final risk: 685.8031
[Fold: 25]
[ 1] ........................................ -- risk: 686.6695
[ 41] ........................................ -- risk: 682.621
[ 81] ........................................ -- risk: 681.4878
[ 121] ........................................ -- risk: 681.0906
[ 161] .......................................
Final risk: 681.3247
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 719.9972
[ 41] ........................................ -- risk: 718.5984
[ 81] ........................................ -- risk: 718.8706
[ 121] ........................................ -- risk: 719.4563
[ 161] .......................................
Final risk: 719.963
[Fold: 2]
[ 1] ........................................ -- risk: 698.6124
[ 41] ........................................ -- risk: 697.1256
[ 81] ........................................ -- risk: 695.9188
[ 121] ........................................ -- risk: 695.1877
[ 161] .......................................
Final risk: 694.9584
[Fold: 3]
[ 1] ........................................ -- risk: 730.1709
[ 41] ........................................ -- risk: 729.1696
[ 81] ........................................ -- risk: 729.8959
[ 121] ........................................ -- risk: 730.4896
[ 161] .......................................
Final risk: 730.9693
[Fold: 4]
[ 1] ........................................ -- risk: 710.0003
[ 41] ........................................ -- risk: 708.6995
[ 81] ........................................ -- risk: 709.1862
[ 121] ........................................ -- risk: 710.4508
[ 161] .......................................
Final risk: 712.7734
[Fold: 5]
[ 1] ........................................ -- risk: 706.5151
[ 41] ........................................ -- risk: 703.3607
[ 81] ........................................ -- risk: 703.4981
[ 121] ........................................ -- risk: 704.2714
[ 161] .......................................
Final risk: 705.1154
[Fold: 6]
[ 1] ........................................ -- risk: 717.4869
[ 41] ........................................ -- risk: 716.1596
[ 81] ........................................ -- risk: 716.2547
[ 121] ........................................ -- risk: 716.6823
[ 161] .......................................
Final risk: 717.7667
[Fold: 7]
[ 1] ........................................ -- risk: 704.3196
[ 41] ........................................ -- risk: 705.5834
[ 81] ........................................ -- risk: 707.2067
[ 121] ........................................ -- risk: 708.0918
[ 161] .......................................
Final risk: 708.1971
[Fold: 8]
[ 1] ........................................ -- risk: 693.9015
[ 41] ........................................ -- risk: 690.6778
[ 81] ........................................ -- risk: 689.8156
[ 121] ........................................ -- risk: 689.7521
[ 161] .......................................
Final risk: 689.8695
[Fold: 9]
[ 1] ........................................ -- risk: 739.3387
[ 41] ........................................ -- risk: 737.4676
[ 81] ........................................ -- risk: 737.5416
[ 121] ........................................ -- risk: 737.9744
[ 161] .......................................
Final risk: 738.7086
[Fold: 10]
[ 1] ........................................ -- risk: 692.1158
[ 41] ........................................ -- risk: 692.2833
[ 81] ........................................ -- risk: 692.3318
[ 121] ........................................ -- risk: 692.0667
[ 161] .......................................
Final risk: 691.8441
[Fold: 11]
[ 1] ........................................ -- risk: 672.1793
[ 41] ........................................ -- risk: 671.4536
[ 81] ........................................ -- risk: 671.3291
[ 121] ........................................ -- risk: 671.5036
[ 161] .......................................
Final risk: 672.2167
[Fold: 12]
[ 1] ........................................ -- risk: 645.8862
[ 41] ........................................ -- risk: 645.5201
[ 81] ........................................ -- risk: 646.1145
[ 121] ........................................ -- risk: 647.1749
[ 161] .......................................
Final risk: 648.3768
[Fold: 13]
[ 1] ........................................ -- risk: 692.4763
[ 41] ........................................ -- risk: 691.8445
[ 81] ........................................ -- risk: 692.5235
[ 121] ........................................ -- risk: 693.0978
[ 161] .......................................
Final risk: 693.4188
[Fold: 14]
[ 1] ........................................ -- risk: 657.314
[ 41] ........................................ -- risk: 658.5194
[ 81] ........................................ -- risk: 659.3122
[ 121] ........................................ -- risk: 659.8841
[ 161] .......................................
Final risk: 660.612
[Fold: 15]
[ 1] ........................................ -- risk: 672.6807
[ 41] ........................................ -- risk: 668.6088
[ 81] ........................................ -- risk: 668.1865
[ 121] ........................................ -- risk: 668.3982
[ 161] .......................................
Final risk: 668.6745
[Fold: 16]
[ 1] ........................................ -- risk: 696.841
[ 41] ........................................ -- risk: 697.3282
[ 81] ........................................ -- risk: 698.3298
[ 121] ........................................ -- risk: 699.3594
[ 161] .......................................
Final risk: 699.9434
[Fold: 17]
[ 1] ........................................ -- risk: 683.9651
[ 41] ........................................ -- risk: 683.1564
[ 81] ........................................ -- risk: 684.0195
[ 121] ........................................ -- risk: 684.3366
[ 161] .......................................
Final risk: 684.5827
[Fold: 18]
[ 1] ........................................ -- risk: 709.0313
[ 41] ........................................ -- risk: 709.3562
[ 81] ........................................ -- risk: 710.6012
[ 121] ........................................ -- risk: 712.3088
[ 161] .......................................
Final risk: 714.2031
[Fold: 19]
[ 1] ........................................ -- risk: 643.8378
[ 41] ........................................ -- risk: 644.3906
[ 81] ........................................ -- risk: 646.1881
[ 121] ........................................ -- risk: 647.3145
[ 161] .......................................
Final risk: 647.5664
[Fold: 20]
[ 1] ........................................ -- risk: 709.7634
[ 41] ........................................ -- risk: 708.5168
[ 81] ........................................ -- risk: 707.3607
[ 121] ........................................ -- risk: 707.0055
[ 161] .......................................
Final risk: 707.0855
[Fold: 21]
[ 1] ........................................ -- risk: 740.8305
[ 41] ........................................ -- risk: 738.4451
[ 81] ........................................ -- risk: 739.6263
[ 121] ........................................ -- risk: 741.2373
[ 161] .......................................
Final risk: 742.8271
[Fold: 22]
[ 1] ........................................ -- risk: 730.7473
[ 41] ........................................ -- risk: 728.8696
[ 81] ........................................ -- risk: 727.519
[ 121] ........................................ -- risk: 726.7112
[ 161] .......................................
Final risk: 726.2656
[Fold: 23]
[ 1] ........................................ -- risk: 620.1569
[ 41] ........................................ -- risk: 619.496
[ 81] ........................................ -- risk: 620.1367
[ 121] ........................................ -- risk: 620.2289
[ 161] .......................................
Final risk: 620.4466
[Fold: 24]
[ 1] ........................................ -- risk: 703.352
[ 41] ........................................ -- risk: 703.1727
[ 81] ........................................ -- risk: 703.2005
[ 121] ........................................ -- risk: 703.1689
[ 161] .......................................
Final risk: 703.005
[Fold: 25]
[ 1] ........................................ -- risk: 725.5837
[ 41] ........................................ -- risk: 724.7946
[ 81] ........................................ -- risk: 725.2691
[ 121] ........................................ -- risk: 727.0454
[ 161] .......................................
Final risk: 729.8365
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 710.7633
[ 41] ........................................ -- risk: 708.6872
[ 81] ........................................ -- risk: 707.4141
[ 121] ........................................ -- risk: 706.3774
[ 161] .......................................
Final risk: 705.7771
[Fold: 2]
[ 1] ........................................ -- risk: 740.2472
[ 41] ........................................ -- risk: 736.8755
[ 81] ........................................ -- risk: 739.7701
[ 121] ........................................ -- risk: 742.7881
[ 161] .......................................
Final risk: 746.1537
[Fold: 3]
[ 1] ........................................ -- risk: 678.9249
[ 41] ........................................ -- risk: 670.8093
[ 81] ........................................ -- risk: 666.9266
[ 121] ........................................ -- risk: 664.6018
[ 161] .......................................
Final risk: 663.1575
[Fold: 4]
[ 1] ........................................ -- risk: 637.9774
[ 41] ........................................ -- risk: 633.6363
[ 81] ........................................ -- risk: 631.8029
[ 121] ........................................ -- risk: 631.1177
[ 161] .......................................
Final risk: 630.7461
[Fold: 5]
[ 1] ........................................ -- risk: 680.3579
[ 41] ........................................ -- risk: 674.1693
[ 81] ........................................ -- risk: 672.1796
[ 121] ........................................ -- risk: 670.654
[ 161] .......................................
Final risk: 669.9729
[Fold: 6]
[ 1] ........................................ -- risk: 660.2937
[ 41] ........................................ -- risk: 657.4505
[ 81] ........................................ -- risk: 656.5306
[ 121] ........................................ -- risk: 655.9328
[ 161] .......................................
Final risk: 655.0751
[Fold: 7]
[ 1] ........................................ -- risk: 681.6805
[ 41] ........................................ -- risk: 676.8869
[ 81] ........................................ -- risk: 675.2484
[ 121] ........................................ -- risk: 675.4452
[ 161] .......................................
Final risk: 676.1534
[Fold: 8]
[ 1] ........................................ -- risk: 705.4509
[ 41] ........................................ -- risk: 703.2333
[ 81] ........................................ -- risk: 702.706
[ 121] ........................................ -- risk: 703.5539
[ 161] .......................................
Final risk: 704.3427
[Fold: 9]
[ 1] ........................................ -- risk: 625.6541
[ 41] ........................................ -- risk: 622.3469
[ 81] ........................................ -- risk: 620.4757
[ 121] ........................................ -- risk: 618.956
[ 161] .......................................
Final risk: 617.8817
[Fold: 10]
[ 1] ........................................ -- risk: 715.1207
[ 41] ........................................ -- risk: 711.4932
[ 81] ........................................ -- risk: 711.8853
[ 121] ........................................ -- risk: 714.2415
[ 161] .......................................
Final risk: 717.8687
[Fold: 11]
[ 1] ........................................ -- risk: 747.249
[ 41] ........................................ -- risk: 743.3933
[ 81] ........................................ -- risk: 742.5154
[ 121] ........................................ -- risk: 742.7841
[ 161] .......................................
Final risk: 743.2816
[Fold: 12]
[ 1] ........................................ -- risk: 746.9807
[ 41] ........................................ -- risk: 742.583
[ 81] ........................................ -- risk: 740.9737
[ 121] ........................................ -- risk: 740.8157
[ 161] .......................................
Final risk: 741.261
[Fold: 13]
[ 1] ........................................ -- risk: 745.6359
[ 41] ........................................ -- risk: 739.2961
[ 81] ........................................ -- risk: 736.8676
[ 121] ........................................ -- risk: 735.1271
[ 161] .......................................
Final risk: 734.2903
[Fold: 14]
[ 1] ........................................ -- risk: 698.2367
[ 41] ........................................ -- risk: 695.4795
[ 81] ........................................ -- risk: 695.4435
[ 121] ........................................ -- risk: 696.3882
[ 161] .......................................
Final risk: 698.2112
[Fold: 15]
[ 1] ........................................ -- risk: 686.2563
[ 41] ........................................ -- risk: 680.8386
[ 81] ........................................ -- risk: 678.3256
[ 121] ........................................ -- risk: 676.1955
[ 161] .......................................
Final risk: 674.9694
[Fold: 16]
[ 1] ........................................ -- risk: 688.5155
[ 41] ........................................ -- risk: 684.6933
[ 81] ........................................ -- risk: 682.9923
[ 121] ........................................ -- risk: 681.3683
[ 161] .......................................
Final risk: 680.3081
[Fold: 17]
[ 1] ........................................ -- risk: 729.3273
[ 41] ........................................ -- risk: 725.4325
[ 81] ........................................ -- risk: 723.1116
[ 121] ........................................ -- risk: 721.9639
[ 161] .......................................
Final risk: 721.7116
[Fold: 18]
[ 1] ........................................ -- risk: 716.9037
[ 41] ........................................ -- risk: 711.1014
[ 81] ........................................ -- risk: 707.8822
[ 121] ........................................ -- risk: 705.9605
[ 161] .......................................
Final risk: 704.9449
[Fold: 19]
[ 1] ........................................ -- risk: 659.9156
[ 41] ........................................ -- risk: 656.1972
[ 81] ........................................ -- risk: 655.2439
[ 121] ........................................ -- risk: 654.4993
[ 161] .......................................
Final risk: 654.0278
[Fold: 20]
[ 1] ........................................ -- risk: 712.1334
[ 41] ........................................ -- risk: 710.7159
[ 81] ........................................ -- risk: 710.4666
[ 121] ........................................ -- risk: 711.7057
[ 161] .......................................
Final risk: 712.9464
[Fold: 21]
[ 1] ........................................ -- risk: 658.7818
[ 41] ........................................ -- risk: 655.5012
[ 81] ........................................ -- risk: 653.8698
[ 121] ........................................ -- risk: 653.471
[ 161] .......................................
Final risk: 653.2161
[Fold: 22]
[ 1] ........................................ -- risk: 700.1524
[ 41] ........................................ -- risk: 696.4447
[ 81] ........................................ -- risk: 696.8683
[ 121] ........................................ -- risk: 699.3966
[ 161] .......................................
Final risk: 703.6544
[Fold: 23]
[ 1] ........................................ -- risk: 692.3089
[ 41] ........................................ -- risk: 688.1304
[ 81] ........................................ -- risk: 685.98
[ 121] ........................................ -- risk: 684.658
[ 161] .......................................
Final risk: 683.9278
[Fold: 24]
[ 1] ........................................ -- risk: 672.4598
[ 41] ........................................ -- risk: 668.0859
[ 81] ........................................ -- risk: 666.4601
[ 121] ........................................ -- risk: 665.9717
[ 161] .......................................
Final risk: 666.2725
[Fold: 25]
[ 1] ........................................ -- risk: 683.1866
[ 41] ........................................ -- risk: 684.3859
[ 81] ........................................ -- risk: 688.5292
[ 121] ........................................ -- risk: 692.6752
[ 161] .......................................
Final risk: 696.8761
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 709.664
[ 41] ........................................ -- risk: 705.5434
[ 81] ........................................ -- risk: 703.7723
[ 121] ........................................ -- risk: 702.698
[ 161] .......................................
Final risk: 702.2732
[Fold: 2]
[ 1] ........................................ -- risk: 683.8862
[ 41] ........................................ -- risk: 687.5037
[ 81] ........................................ -- risk: 692.7518
[ 121] ........................................ -- risk: 696.5264
[ 161] .......................................
Final risk: 699.1188
[Fold: 3]
[ 1] ........................................ -- risk: 669.0589
[ 41] ........................................ -- risk: 664.0033
[ 81] ........................................ -- risk: 662.1996
[ 121] ........................................ -- risk: 661.1466
[ 161] .......................................
Final risk: 660.8258
[Fold: 4]
[ 1] ........................................ -- risk: 704.0213
[ 41] ........................................ -- risk: 707.3887
[ 81] ........................................ -- risk: 711.8084
[ 121] ........................................ -- risk: 715.3945
[ 161] .......................................
Final risk: 718.6713
[Fold: 5]
[ 1] ........................................ -- risk: 673.017
[ 41] ........................................ -- risk: 667.6108
[ 81] ........................................ -- risk: 666.6483
[ 121] ........................................ -- risk: 665.7551
[ 161] .......................................
Final risk: 665.3176
[Fold: 6]
[ 1] ........................................ -- risk: 694.389
[ 41] ........................................ -- risk: 694.1697
[ 81] ........................................ -- risk: 695.204
[ 121] ........................................ -- risk: 696.739
[ 161] .......................................
Final risk: 698.4591
[Fold: 7]
[ 1] ........................................ -- risk: 698.7408
[ 41] ........................................ -- risk: 697.1753
[ 81] ........................................ -- risk: 697.741
[ 121] ........................................ -- risk: 698.0309
[ 161] .......................................
Final risk: 698.182
[Fold: 8]
[ 1] ........................................ -- risk: 710.4279
[ 41] ........................................ -- risk: 705.312
[ 81] ........................................ -- risk: 704.4762
[ 121] ........................................ -- risk: 705.1375
[ 161] .......................................
Final risk: 705.9193
[Fold: 9]
[ 1] ........................................ -- risk: 739.3122
[ 41] ........................................ -- risk: 738.5607
[ 81] ........................................ -- risk: 742.4557
[ 121] ........................................ -- risk: 746.1238
[ 161] .......................................
Final risk: 748.9031
[Fold: 10]
[ 1] ........................................ -- risk: 750.4386
[ 41] ........................................ -- risk: 746.7067
[ 81] ........................................ -- risk: 744.6021
[ 121] ........................................ -- risk: 743.6301
[ 161] .......................................
Final risk: 743.361
[Fold: 11]
[ 1] ........................................ -- risk: 715.5348
[ 41] ........................................ -- risk: 720.3317
[ 81] ........................................ -- risk: 726.3904
[ 121] ........................................ -- risk: 732.0376
[ 161] .......................................
Final risk: 737.1002
[Fold: 12]
[ 1] ........................................ -- risk: 659.0017
[ 41] ........................................ -- risk: 657.422
[ 81] ........................................ -- risk: 656.5103
[ 121] ........................................ -- risk: 656.2302
[ 161] .......................................
Final risk: 656.2099
[Fold: 13]
[ 1] ........................................ -- risk: 636.5979
[ 41] ........................................ -- risk: 633.7158
[ 81] ........................................ -- risk: 632.855
[ 121] ........................................ -- risk: 632.8627
[ 161] .......................................
Final risk: 633.508
[Fold: 14]
[ 1] ........................................ -- risk: 674.7305
[ 41] ........................................ -- risk: 670.5395
[ 81] ........................................ -- risk: 669.2196
[ 121] ........................................ -- risk: 667.4166
[ 161] .......................................
Final risk: 666.7723
[Fold: 15]
[ 1] ........................................ -- risk: 702.0419
[ 41] ........................................ -- risk: 701.1994
[ 81] ........................................ -- risk: 702.3201
[ 121] ........................................ -- risk: 703.9509
[ 161] .......................................
Final risk: 705.3391
[Fold: 16]
[ 1] ........................................ -- risk: 652.8062
[ 41] ........................................ -- risk: 650.0436
[ 81] ........................................ -- risk: 649.2872
[ 121] ........................................ -- risk: 648.706
[ 161] .......................................
Final risk: 648.6768
[Fold: 17]
[ 1] ........................................ -- risk: 664.7036
[ 41] ........................................ -- risk: 662.0853
[ 81] ........................................ -- risk: 662.6071
[ 121] ........................................ -- risk: 663.9352
[ 161] .......................................
Final risk: 665.3686
[Fold: 18]
[ 1] ........................................ -- risk: 662.3886
[ 41] ........................................ -- risk: 658.718
[ 81] ........................................ -- risk: 657.0836
[ 121] ........................................ -- risk: 655.7694
[ 161] .......................................
Final risk: 654.698
[Fold: 19]
[ 1] ........................................ -- risk: 743.2451
[ 41] ........................................ -- risk: 742.2203
[ 81] ........................................ -- risk: 747.8462
[ 121] ........................................ -- risk: 752.0268
[ 161] .......................................
Final risk: 757.1889
[Fold: 20]
[ 1] ........................................ -- risk: 723.0566
[ 41] ........................................ -- risk: 719.108
[ 81] ........................................ -- risk: 719.3764
[ 121] ........................................ -- risk: 719.7724
[ 161] .......................................
Final risk: 721.6116
[Fold: 21]
[ 1] ........................................ -- risk: 693.8694
[ 41] ........................................ -- risk: 690.0027
[ 81] ........................................ -- risk: 688.2419
[ 121] ........................................ -- risk: 687.8288
[ 161] .......................................
Final risk: 687.7066
[Fold: 22]
[ 1] ........................................ -- risk: 658.7069
[ 41] ........................................ -- risk: 654.1559
[ 81] ........................................ -- risk: 652.1883
[ 121] ........................................ -- risk: 649.9644
[ 161] .......................................
Final risk: 648.2193
[Fold: 23]
[ 1] ........................................ -- risk: 684.5135
[ 41] ........................................ -- risk: 682.06
[ 81] ........................................ -- risk: 680.3232
[ 121] ........................................ -- risk: 679.2456
[ 161] .......................................
Final risk: 678.3274
[Fold: 24]
[ 1] ........................................ -- risk: 684.4296
[ 41] ........................................ -- risk: 684.7654
[ 81] ........................................ -- risk: 685.4241
[ 121] ........................................ -- risk: 686.2357
[ 161] .......................................
Final risk: 687.3806
[Fold: 25]
[ 1] ........................................ -- risk: 695.3296
[ 41] ........................................ -- risk: 691.0055
[ 81] ........................................ -- risk: 688.568
[ 121] ........................................ -- risk: 686.9289
[ 161] .......................................
Final risk: 685.9914
Starting cross-validation...
[Fold: 1]
[ 1] ........................................ -- risk: 682.8275
[ 41] ........................................ -- risk: 680.3269
[ 81] ........................................ -- risk: 678.7878
[ 121] ........................................ -- risk: 678.1265
[ 161] .......................................
Final risk: 677.9985
[Fold: 2]
[ 1] ........................................ -- risk: 698.7833
[ 41] ........................................ -- risk: 697.748
[ 81] ........................................ -- risk: 701.6787
[ 121] ........................................ -- risk: 705.4991
[ 161] .......................................
Final risk: 710.0389
[Fold: 3]
[ 1] ........................................ -- risk: 676.7112
[ 41] ........................................ -- risk: 674.8962
[ 81] ........................................ -- risk: 673.9034
[ 121] ........................................ -- risk: 673.7061
[ 161] .......................................
Final risk: 673.8062
[Fold: 4]
[ 1] ........................................ -- risk: 766.4703
[ 41] ........................................ -- risk: 764.1574
[ 81] ........................................ -- risk: 764.8781
[ 121] ........................................ -- risk: 766.3595
[ 161] .......................................
Final risk: 767.6524
[Fold: 5]
[ 1] ........................................ -- risk: 641.8665
[ 41] ........................................ -- risk: 638.7858
[ 81] ........................................ -- risk: 638.244
[ 121] ........................................ -- risk: 638.0153
[ 161] .......................................
Final risk: 638.414
[Fold: 6]
[ 1] ........................................ -- risk: 725.6877
[ 41] ........................................ -- risk: 724.5403
[ 81] ........................................ -- risk: 723.6831
[ 121] ........................................ -- risk: 724.5359
[ 161] .......................................
Final risk: 724.9115
[Fold: 7]
[ 1] ........................................ -- risk: 680.8669
[ 41] ........................................ -- risk: 678.722
[ 81] ........................................ -- risk: 679.2989
[ 121] ........................................ -- risk: 681.1188
[ 161] .......................................
Final risk: 683.9398
[Fold: 8]
[ 1] ........................................ -- risk: 739.4187
[ 41] ........................................ -- risk: 738.944
[ 81] ........................................ -- risk: 743.173
[ 121] ........................................ -- risk: 747.7499
[ 161] .......................................
Final risk: 752.0823
[Fold: 9]
[ 1] ........................................ -- risk: 723.3883
[ 41] ........................................ -- risk: 729.8939
[ 81] ........................................ -- risk: 740.6584
[ 121] ........................................ -- risk: 747.6464
[ 161] .......................................
Final risk: 756.9946
[Fold: 10]
[ 1] ........................................ -- risk: 694.9165
[ 41] ........................................ -- risk: 695.6152
[ 81] ........................................ -- risk: 699.7636
[ 121] ........................................ -- risk: 705.7099
[ 161] .......................................
Final risk: 709.3841
[Fold: 11]
[ 1] ........................................ -- risk: 694.2689
[ 41] ........................................ -- risk: 693.3089
[ 81] ........................................ -- risk: 695.0009
[ 121] ........................................ -- risk: 698.4475
[ 161] .......................................
Final risk: 703.6773
[Fold: 12]
[ 1] ........................................ -- risk: 659.5791
[ 41] ........................................ -- risk: 655.9375
[ 81] ........................................ -- risk: 653.451
[ 121] ........................................ -- risk: 651.5276
[ 161] .......................................
Final risk: 650.6361
[Fold: 13]
[ 1] ........................................ -- risk: 679.5196
[ 41] ........................................ -- risk: 674.3434
[ 81] ........................................ -- risk: 671.6306
[ 121] ........................................ -- risk: 669.3722
[ 161] .......................................
Final risk: 667.9082
[Fold: 14]
[ 1] ........................................ -- risk: 672.9346
[ 41] ........................................ -- risk: 670.048
[ 81] ........................................ -- risk: 667.8636
[ 121] ........................................ -- risk: 666.5861
[ 161] .......................................
Final risk: 665.6434
[Fold: 15]
[ 1] ........................................ -- risk: 655.0938
[ 41] ........................................ -- risk: 662.4603
[ 81] ........................................ -- risk: 670.6938
[ 121] ........................................ -- risk: 677.6624
[ 161] .......................................
Final risk: 682.6085
[Fold: 16]
[ 1] ........................................ -- risk: 661.3601
[ 41] ........................................ -- risk: 663.8131
[ 81] ........................................ -- risk: 667.7377
[ 121] ........................................ -- risk: 671.3152
[ 161] .......................................
Final risk: 673.9312
[Fold: 17]
[ 1] ........................................ -- risk: 737.7693
[ 41] ........................................ -- risk: 732.5311
[ 81] ........................................ -- risk: 730.0717
[ 121] ........................................ -- risk: 728.7775
[ 161] .......................................
Final risk: 728.4456
[Fold: 18]
[ 1] ........................................ -- risk: 692.1021
[ 41] ........................................ -- risk: 688.3127
[ 81] ........................................ -- risk: 686.3368
[ 121] ........................................ -- risk: 685.1643
[ 161] .......................................
Final risk: 684.4109
[Fold: 19]
[ 1] ........................................ -- risk: 697.4113
[ 41] ........................................ -- risk: 696.6692
[ 81] ........................................ -- risk: 698.904
[ 121] ........................................ -- risk: 701.6554
[ 161] .......................................
Final risk: 705.9758
[Fold: 20]
[ 1] ........................................ -- risk: 704.521
[ 41] ........................................ -- risk: 701.875
[ 81] ........................................ -- risk: 704.6186
[ 121] ........................................ -- risk: 708.9825
[ 161] .......................................
Final risk: 711.8929
[Fold: 21]
[ 1] ........................................ -- risk: 719.1269
[ 41] ........................................ -- risk: 717.75
[ 81] ........................................ -- risk: 719.5138
[ 121] ........................................ -- risk: 720.749
[ 161] .......................................
Final risk: 722.3501
[Fold: 22]
[ 1] ........................................ -- risk: 644.7593
[ 41] ........................................ -- risk: 639.9175
[ 81] ........................................ -- risk: 638.147
[ 121] ........................................ -- risk: 637.6662
[ 161] .......................................
Final risk: 637.4669
[Fold: 23]
[ 1] ........................................ -- risk: 698.8517
[ 41] ........................................ -- risk: 696.8774
[ 81] ........................................ -- risk: 695.2376
[ 121] ........................................ -- risk: 694.9442
[ 161] .......................................
Final risk: 695.6362
[Fold: 24]
[ 1] ........................................ -- risk: 649.5938
[ 41] ........................................ -- risk: 646.4291
[ 81] ........................................ -- risk: 644.1593
[ 121] ........................................ -- risk: 642.3895
[ 161] .......................................
Final risk: 641.6822
[Fold: 25]
[ 1] ........................................ -- risk: 737.3172
[ 41] ........................................ -- risk: 735.737
[ 81] ........................................ -- risk: 739.139
[ 121] ........................................ -- risk: 744.6437
[ 161] .......................................
Final risk: 750.5538 MAPE <- median(100*abs((kfold.boost$pred-kfold.boost$y)/(kfold.boost$y+1)))
MSEP <- mean((kfold.boost$pred-kfold.boost$y)^2)
MAPE[1] 67.87735MSEP[1] 1784.676Evaluation of MAPE and MSEP for model m.NN:
kfold.NN <- kCV(model=m.NN, data=fbdata, K=10, seed=2345)We encountered a problem in that the command
mtrain <- update(model, data=training.data)does not work for the m.NN model (even though it worked for m.SICHEL). Even more strange, it worked when stepping through the commands manually. We will attempt to fix this, but in the meantime kfold.NN was obtained by stepping through kCV() manually.
MAPE <- median(100*abs((kfold.NN$pred-kfold.NN$y)/(kfold.NN$y+1)))
MSEP <- mean((kfold.NN$pred-kfold.NN$y)^2)
MAPE[1] 59.62527MSEP[1] 1785.128CRPS
kCRPS <- function(model, data, K, seed, ymax=150)
{
I <- kfold(data, K, seed) # vector of indices for K folds
data$row <- 1:nrow(data)
y <- 0:ymax
predicted <- data.frame(row=1:nrow(data), y=model$y, mu=NA, sigma=NA, nu=NA)
predicted[,6:(6+ymax)] <- NA
for(k in 1:K)
{
Itrain <- I!=k
training.data <- data[Itrain,]
test.data <- data[!Itrain,]
mtrain <- try(update(model, data=training.data)) # doesn't work for NN model
predtest <- predictAll(mtrain, data=training.data, newdata=test.data, type="response")
predicted[test.data$row, "mu"] <- predtest$mu
predicted[test.data$row, "sigma"] <- predtest$sigma
predicted[test.data$row, "nu"] <- predtest$nu
}
for(yi in y) predicted[,6+yi] <-
(pSICHEL(yi, predicted$mu, predicted$sigma, predicted$nu)-as.numeric(yi>=predicted$y))^2
predicted$CRPS <- -rowSums(predicted[,-(1:5)])
return(sum(predicted$CRPS))
}crps <- kCRPS(model=m.SICHEL, data=fbdata, K=10, seed=2345, ymax=791)crps[1] -6259.246Again the cross-validation did not work for model m.NN and CRPS had to be obtained manually.
Log score
We use the gamlss function gamlssCV() to extract the log scores.
Model m.SICHEL
m.SICHEL.CV <- gamlssCV(formula = share ~ Category + Type + pbc(Post.Weekday) +
pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour),
sigma.formula = ~Category +
pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Hour) + pbc(Post.Weekday),
nu.formula = ~ Category + Type +
pbc(Post.Month, control = pbc.control(inter = 5)) +
pbc(Post.Weekday) + pbc(Post.Hour),
family = SICHEL, data = fbdata, method = mixed(20, 100),
K.fold=10, set.seed=123)m.SICHEL.CV$CV/(-2) # log likelihood[1] -2064.038Model m.NN
The gamlssCV() function does not work for models including nn() terms:
m2 <- gamlssCV(share ~ nn(~ Category.s + Post.Weekday.s + Post.Month.s +
Post.Hour.s + type3, size=3, decay=0.1),
sigma.formula = ~ nn(~ Category.s + Post.Weekday.s +
Post.Month.s + Post.Hour.s + type3, size=3, decay=0.1),
nu.formula = nn(~Category.s + Post.Weekday.s + Post.Month.s +
Post.Hour.s + type3, size=3, decay=0.1),
family = SICHEL, data = fbdata, n.cyc=200,
K.fold=10, set.seed=123)At present we have to step through the computations manually. (Hopefully this will be fixed.)
Figure 10.4: Term plots for Category and Post.Month
term.plot(m.SICHEL, what="mu", pages=1, ylim="common",
terms=c("Category", "pbc(Post.Month, control = pbc.control(inter = 5))"),
ylab=c("Partial for Category","Partial for pbc(Post.Month)"), mar=c(4, 1, 1, 2) + 0.1)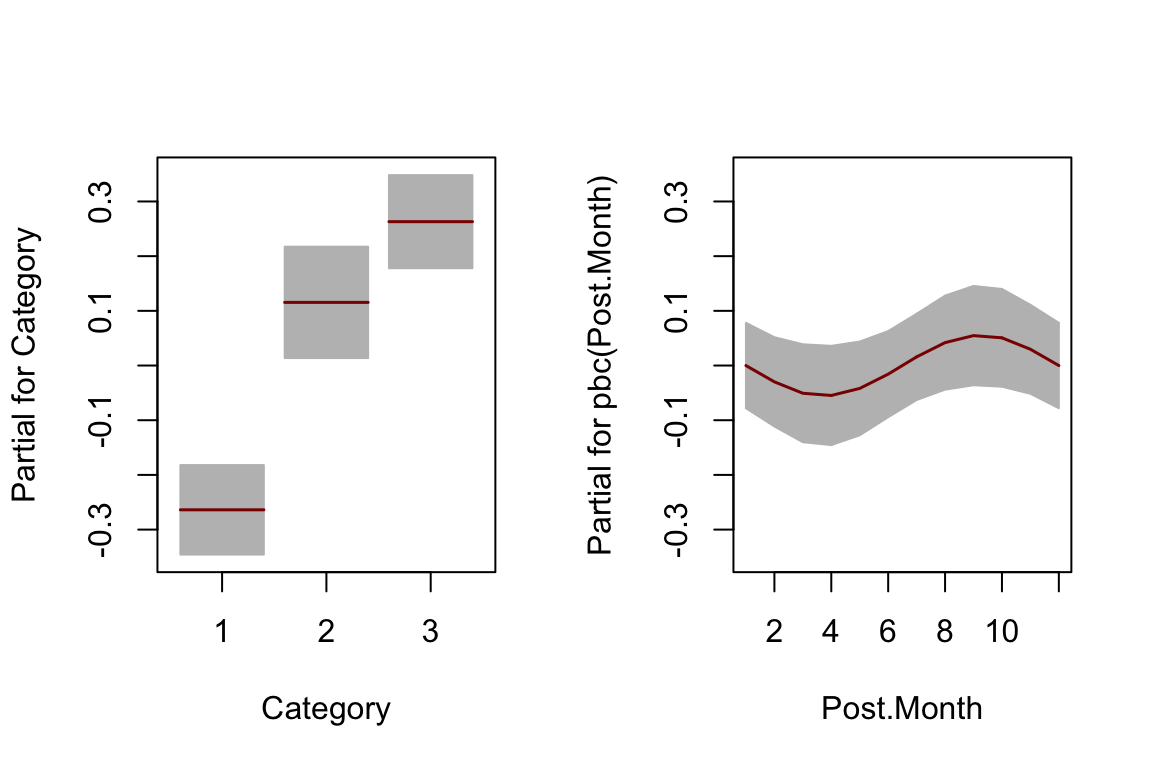
term.plot(m.SICHEL, what="sigma", pages=1, ylim="common",
terms=c("Category", "pbc(Post.Month, control = pbc.control(inter = 5))"),
ylab=c("Partial for Category","Partial for pbc(Post.Month)"))
term.plot(m.SICHEL, what="nu", pages=1, ylim="common",
terms=c("Category", "pbc(Post.Month, control = pbc.control(inter = 5))"),
ylab=c("Partial for Category","Partial for pbc(Post.Month)"))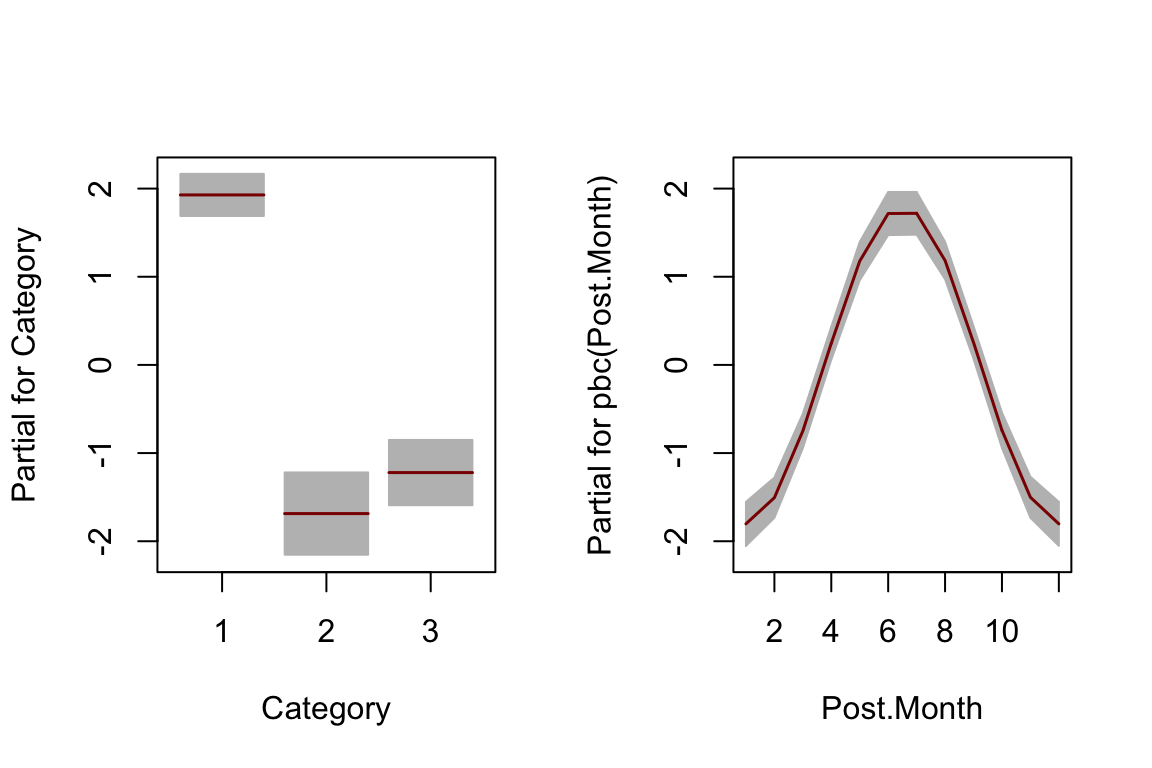
Figure 10.5: Plots of fitted response distribution
library(distreg.vis)These plots were created using the distreg.vis package, which is interactive. The following is the code generated by the package.
(a) Category
The following scenarios were selected: Post.Month = 10 (October), Post.Weekday = 6 (Friday), Post.Hour = 3, Type = “Photo/Video”, Category = 1, 2, 3 (“action”, “product”, “inspiration”).
covariate_data <- structure(list(Post.Month = c(10L, 10L, 10L),
Post.Weekday = c(6L, 6L, 6L),
Post.Hour = c(3L, 3L, 3L),
Category = structure(c(1L, 2L, 3L),
levels = c("1", "2", "3"), class = "factor"),
Type = c("Photo/Video", "Photo/Video", "Photo/Video")),
class = "data.frame",
row.names = c("1 action", "2 product", "3 inspiration"))
pred_data <- preds(model = m.SICHEL, newdata = covariate_data)
plot_dist(model = m.SICHEL, pred_params = pred_data, type = "pdf", palette = "Set1") +
lims(x=c(0,150)) +
labs(title=NULL) +
guides(fill=guide_legend(title='Category')) +
theme(text = element_text(size=14))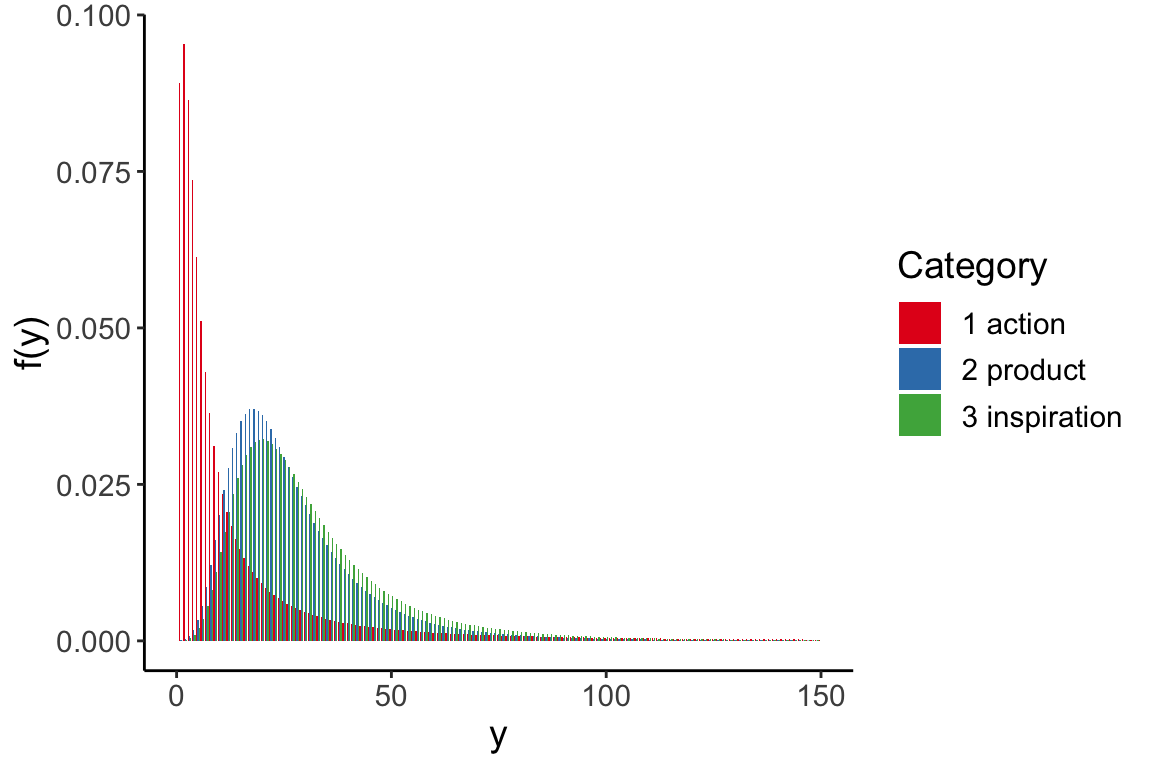
(b) Month
The following scenarios were selected: Post.Month = 1, 5, 10 (January, May, October), Post.Weekday = 6 (Friday), Post.Hour = 3, Category = 1 (“action”), Type = “Photo/Video”.
covariate_data <- structure(list(Post.Month = c(1L, 5L, 10L),
Post.Weekday = c(6L, 6L, 6L),
Post.Hour = c(3L, 3L, 3L),
Category = structure(c(1L, 1L, 1L),
levels = c("1", "2", "3"), class = "factor"),
Type = c("Photo/Video", "Photo/Video", "Photo/Video")),
class = "data.frame",
row.names = c("January", "May", "October"))
pred_data <- preds(model = m.SICHEL, newdata = covariate_data)
plot_dist(model = m.SICHEL, pred_params = pred_data, type = "pdf", palette = "Set1") +
lims(x=c(0,150)) +
labs(title=NULL) +
guides(fill=guide_legend(title='Month')) +
theme(text = element_text(size=14))