library(gamlss)
library(gamlss.ggplots)
#library(gamlss.prepdata)
library(gamlss.foreach)
library(ggplot2)8: Fetal Ultrasound
Figure 8.1
load(file="data/Ultra.RData")
y_hist(ultra$birthweight, title="")+xlab("birthweight (g)")+
theme_bw(base_size = 15) 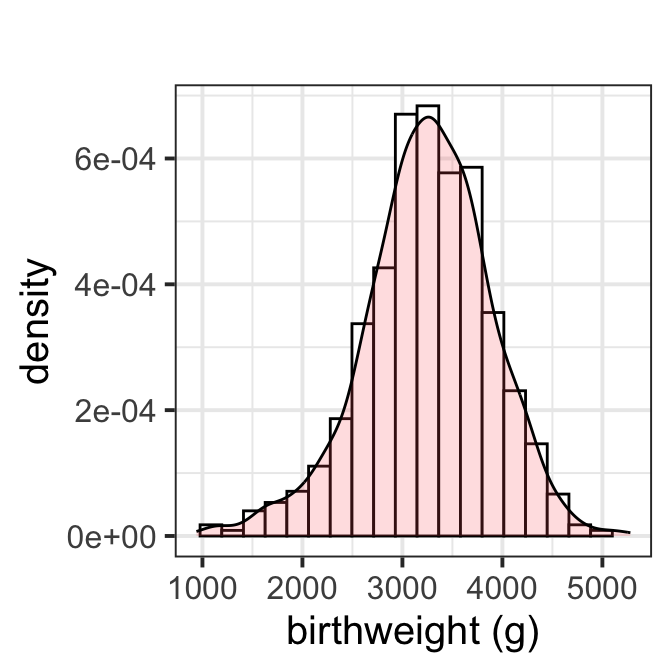
Figure 8.2 a
ggplot(data=ultra, aes(x=AC , y=birthweight))+geom_point(size=1)+
geom_smooth(col="black")+theme_bw(base_size = 15)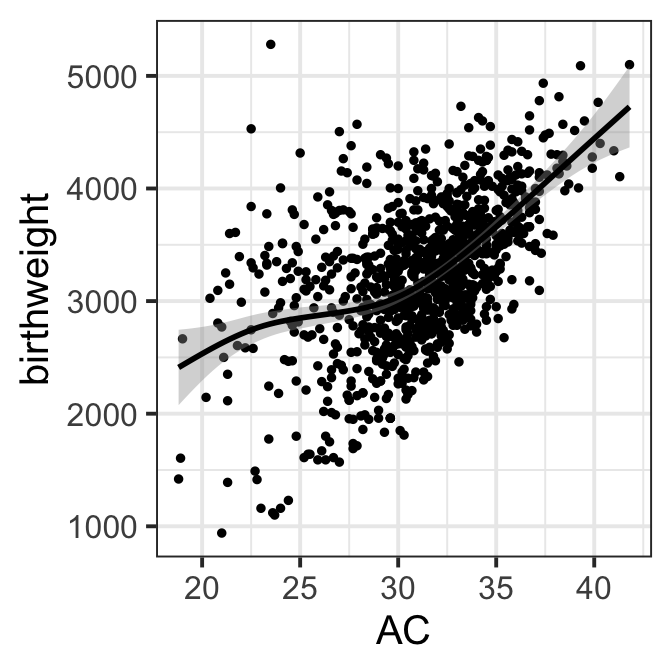
Figure 8.2 b
ggplot(data=ultra, aes(x=HC,y=birthweight))+geom_point(size=1)+
geom_smooth(col="black")+ theme_bw(base_size = 15)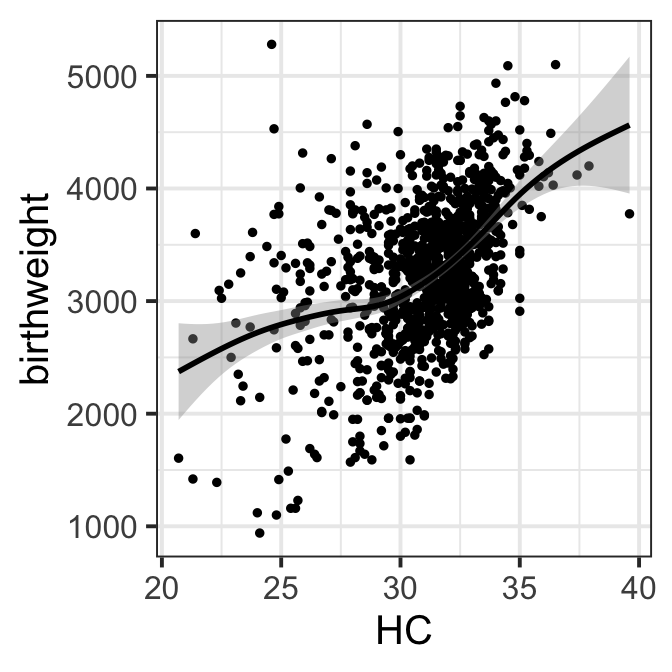
Figure 8.2 c
ggplot(data=ultra, aes(x=FL,y=birthweight))+geom_point(size=1)+
geom_smooth(col="black")+theme_bw(base_size = 15)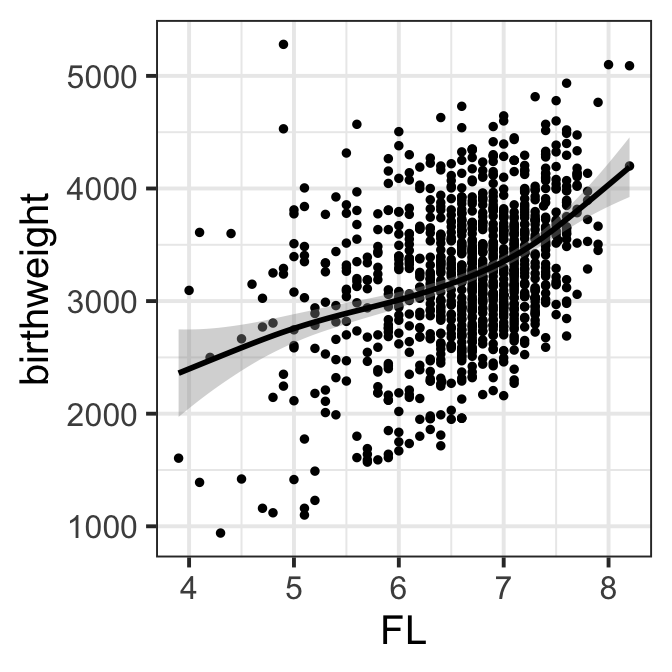
Figure 8.2 d
ggplot(data=ultra)+geom_boxplot(aes(x=parity, y=birthweight))+
theme_bw(base_size = 15)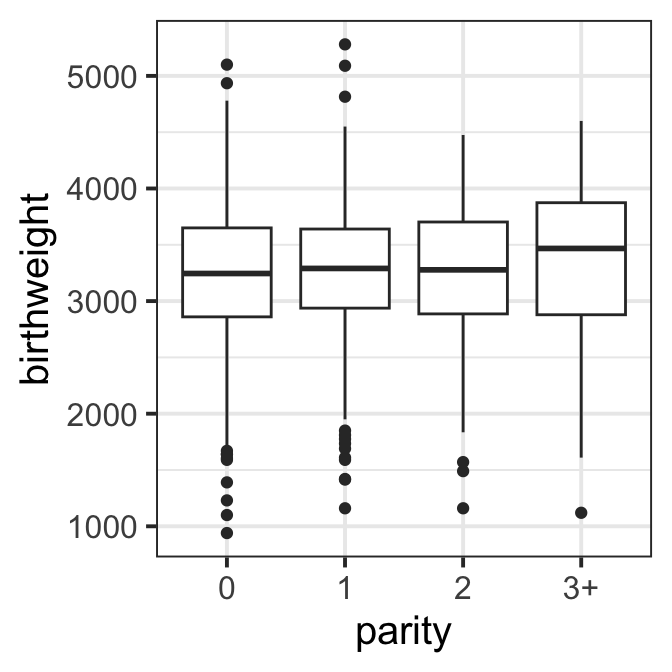
Figure 8.2 e
ggplot(data=ultra, aes(x=age,y=birthweight))+geom_point(size=1) +
geom_smooth(col="black")+ theme_bw(base_size = 15)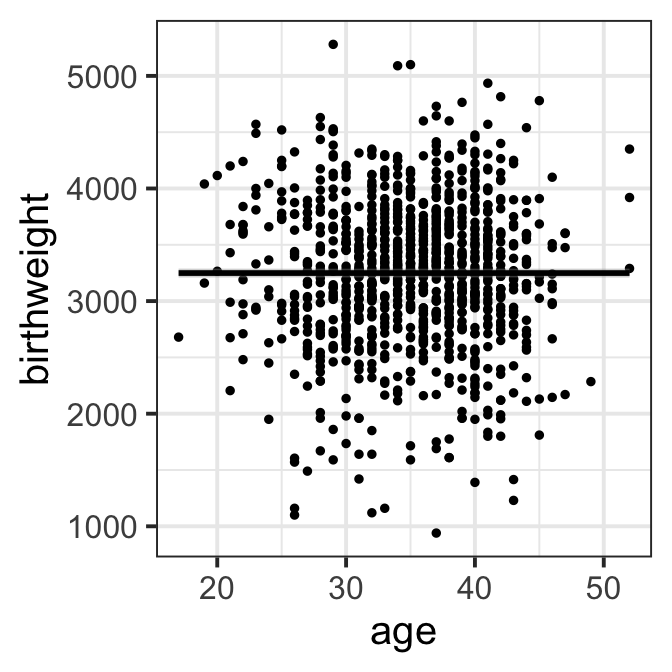
Figure 8.2 f
ggplot(data=ultra, aes(x=DBD,y=birthweight))+geom_point(size=1) +
geom_smooth(col="black")+theme_bw(base_size = 15)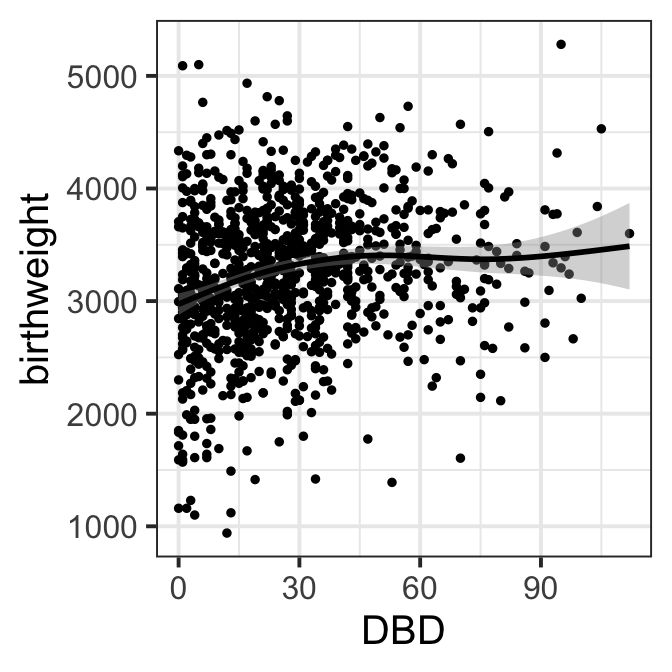
Figure 8.3
library(GGally)
ggpairs(ultra, columns=c(1,2,3,4,6,8) )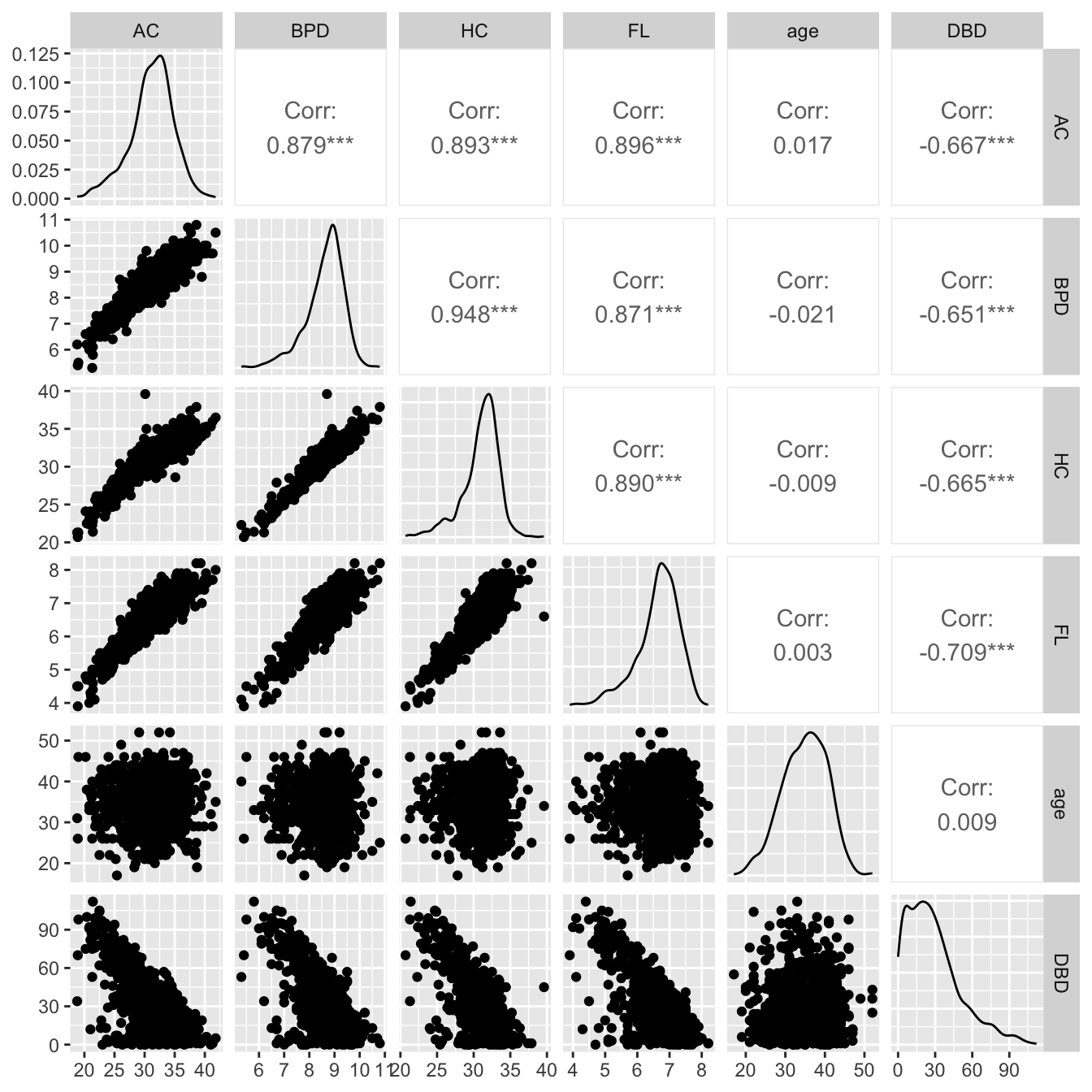
Table 8.1
Fitting the original models and creation of Table 8.1
nullmodel <- gamlss(birthweight~1,sigma.fo=~1, data=ultra, family=NO, trace=FALSE)
LM1 <- gamlss(birthweight~.,sigma.fo=~., data=ultra, family=NO, trace=FALSE)
LM2 <- gamlss(birthweight~(AC+BPD+HC+FL+parity+age+DBD)^2,
sigma.fo=~(AC+BPD+HC+FL+parity+age+DBD)^2,
data=ultra, family=NO, n.cyc=50, trace=FALSE)
GAIC.table(nullmodel,LM1, LM2, k=c(0,2,6.95))minimum GAIC(k= 0 ) model: LM2
minimum GAIC(k= 2 ) model: LM2
minimum GAIC(k= 6.95 ) model: LM1 df k=0 k=2 k=6.95
nullmodel 2 16339.21 16343.21 16353.11
LM1 20 14696.32 14736.32 14835.32
LM2 86 14545.93 14717.93 15143.63Table 8.2
summary(LM1)******************************************************************
Family: c("NO", "Normal")
Call: gamlss(formula = birthweight ~ ., sigma.formula = ~.,
family = NO, data = ultra, trace = FALSE)
Fitting method: RS()
------------------------------------------------------------------
Mu link function: identity
Mu Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4624.3385 172.8716 -26.750 < 2e-16 ***
AC 152.8162 6.2379 24.498 < 2e-16 ***
BPD 97.2317 33.5380 2.899 0.003822 **
HC 24.5465 10.4863 2.341 0.019434 *
FL 120.6880 34.4017 3.508 0.000471 ***
parity1 59.5231 20.5917 2.891 0.003926 **
parity2 61.2613 30.6683 1.998 0.046032 *
parity3+ 141.4639 39.5003 3.581 0.000358 ***
age -3.7268 1.6165 -2.306 0.021338 *
DBD 28.5806 0.5979 47.805 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.717944 0.477468 11.976 < 2e-16 ***
AC 0.037066 0.017004 2.180 0.02950 *
BPD 0.273322 0.098840 2.765 0.00579 **
HC -0.092955 0.035093 -2.649 0.00820 **
FL -0.105585 0.090566 -1.166 0.24396
parity1 0.021205 0.051701 0.410 0.68179
parity2 0.040590 0.076673 0.529 0.59665
parity3+ -0.085410 0.107307 -0.796 0.42625
age -0.004997 0.004208 -1.188 0.23529
DBD 0.006384 0.001470 4.343 1.55e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
No. of observations in the fit: 1038
Degrees of Freedom for the fit: 20
Residual Deg. of Freedom: 1018
at cycle: 5
Global Deviance: 14696.32
AIC: 14736.32
SBC: 14835.22
******************************************************************Table 8.3
drop1(LM1, parameter="sigma")Single term deletions for
sigma
Model:
birthweight ~ AC + BPD + HC + FL + parity + age + DBD
Df AIC LRT Pr(Chi)
<none> 14736
AC 1 14739 4.7696 0.028967 *
BPD 1 14742 7.5346 0.006052 **
HC 1 14741 6.8608 0.008811 **
FL 1 14736 1.3647 0.242719
parity 3 14732 1.1844 0.756749
age 1 14736 1.4045 0.235965
DBD 1 14752 17.9264 2.296e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Table 8.4
GAIC(nullmodel,LM1, k=0) df AIC
LM1 20 14696.32
nullmodel 2 16339.21LR.test(nullmodel,LM1) Likelihood Ratio Test for nested GAMLSS models.
(No check whether the models are nested is performed).
Null model: deviance= 16339.21 with 2 deg. of freedom
Altenative model: deviance= 14696.32 with 20 deg. of freedom
LRT = 1642.886 with 18 deg. of freedom and p-value= 0 Figure 8.4: Confidence intervals
Figure 8.4 was constructed from outputs which use different techniques. Here first we reproduce the results and then we plot the figure. Note in the cases that we need to simulate or re-sample the data, the results could be slightly different from the ones in the book.
The Wald and the robust CI’s:
# Wald
confint(LM1, parameter="sigma")[2,] 2.5 % 97.5 %
0.003738496 0.070392600 # Robust
confint(LM1, parameter="sigma", robust=TRUE)[2,] 2.5 % 97.5 %
-0.007229057 0.081360152 Bootstrapping:
# non-parametric bootstrapping
library(doParallel)
library(gamlss.foreach)
# here use how many cores your computer has
# ours has 10
registerDoParallel(cores = 10)
set.seed(123)
B1 <- NonParametricBoot(LM1, B=1000)
C1 <- summary(B1, show=FALSE)
Coefficients from nonparam.boot() taken from: 1000 simulations
mean 2.5% 50% 97.5% mle
mu.(Intercept) -4.6218e+03 -4.9642e+03 -4.6183e+03 -4.2892e+03 -4624.3385
mu.AC 1.5310e+02 1.4153e+02 1.5311e+02 1.6413e+02 152.8162
mu.BPD 9.6034e+01 2.7391e+01 9.5585e+01 1.6757e+02 97.2317
mu.HC 2.4643e+01 2.7576e+00 2.5315e+01 4.4855e+01 24.5465
mu.FL 1.2025e+02 5.5233e+01 1.2098e+02 1.8834e+02 120.6880
mu.parity1 5.9206e+01 1.9458e+01 5.9555e+01 9.9812e+01 59.5231
mu.parity2 6.0392e+01 1.4911e+00 5.8775e+01 1.2508e+02 61.2613
mu.parity3+ 1.3995e+02 6.5882e+01 1.3950e+02 2.1744e+02 141.4639
mu.age -3.7656e+00 -6.8945e+00 -3.7514e+00 -7.0254e-01 -3.7268
mu.DBD 2.8583e+01 2.7367e+01 2.8579e+01 2.9811e+01 28.5806
sigma.(Intercept) 5.6568e+00 4.7328e+00 5.6426e+00 6.5822e+00 5.7179
sigma.AC 3.9768e-02 -2.2541e-03 4.0382e-02 8.6431e-02 0.0371
sigma.BPD 2.5068e-01 -6.1837e-02 2.5948e-01 5.3056e-01 0.2733
sigma.HC -8.5051e-02 -1.8212e-01 -8.2541e-02 6.7830e-03 -0.0930
sigma.FL -1.1995e-01 -3.5676e-01 -1.1850e-01 9.3054e-02 -0.1056
sigma.parity1 1.7807e-02 -1.0135e-01 1.7189e-02 1.3972e-01 0.0212
sigma.parity2 3.2712e-02 -1.5312e-01 3.8483e-02 2.0587e-01 0.0406
sigma.parity3+ -1.0538e-01 -3.3392e-01 -9.8039e-02 1.0095e-01 -0.0854
sigma.age -4.7646e-03 -1.4317e-02 -4.5515e-03 3.9747e-03 -0.0050
sigma.DBD 6.5800e-03 3.2803e-03 6.6371e-03 1.0039e-02 0.0064
deviance 1.4671e+04 1.4558e+04 1.4673e+04 1.4780e+04 14696.3213C1[12,][c(2,4)] 2.5% 97.5%
-0.002254119 0.086431316 # Bayesian bootstrapping
B2 <- BayesianBoot(LM1, B=1000)
C2 <- summary(B2, show=FALSE)
Coefficients from Baysian.boot() taken from: 1000 simulations
mean 2.5% 50% 97.5% mle
mu.(Intercept) -4.6189e+03 -4.9554e+03 -4.6164e+03 -4.2831e+03 -4624.3385
mu.AC 1.5324e+02 1.4199e+02 1.5323e+02 1.6419e+02 152.8162
mu.BPD 9.8481e+01 3.6271e+01 9.8938e+01 1.6601e+02 97.2317
mu.HC 2.3694e+01 2.4061e+00 2.4599e+01 4.2370e+01 24.5465
mu.FL 1.2038e+02 5.9618e+01 1.2189e+02 1.8090e+02 120.6880
mu.parity1 5.9117e+01 2.0350e+01 5.8405e+01 9.9464e+01 59.5231
mu.parity2 6.0713e+01 1.4939e+00 6.0452e+01 1.2143e+02 61.2613
mu.parity3+ 1.4052e+02 6.7801e+01 1.3743e+02 2.1740e+02 141.4639
mu.age -3.7666e+00 -6.8183e+00 -3.7725e+00 -1.1861e+00 -3.7268
mu.DBD 2.8597e+01 2.7419e+01 2.8591e+01 2.9758e+01 28.5806
sigma.(Intercept) 5.6817e+00 4.7566e+00 5.6889e+00 6.5494e+00 5.7179
sigma.AC 3.8982e-02 -3.2529e-03 3.8606e-02 8.1516e-02 0.0371
sigma.BPD 2.5903e-01 3.5062e-03 2.6134e-01 5.2525e-01 0.2733
sigma.HC -8.7164e-02 -1.7162e-01 -8.7194e-02 -1.7404e-03 -0.0930
sigma.FL -1.2047e-01 -3.1875e-01 -1.2180e-01 7.5698e-02 -0.1056
sigma.parity1 1.5981e-02 -9.7465e-02 1.6978e-02 1.3047e-01 0.0212
sigma.parity2 3.2647e-02 -1.3632e-01 3.0015e-02 2.1040e-01 0.0406
sigma.parity3+ -1.0176e-01 -3.1931e-01 -1.0121e-01 9.9876e-02 -0.0854
sigma.age -4.7239e-03 -1.3154e-02 -4.6557e-03 3.8866e-03 -0.0050
sigma.DBD 6.4304e-03 3.6364e-03 6.4008e-03 9.3133e-03 0.0064
deviance 1.4671e+04 1.4564e+04 1.4671e+04 1.4777e+04 14696.3213C2[12,][c(2,4)] 2.5% 97.5%
-0.00325290 0.08151643 Profile likelihood:
mod1 <- quote(gamlss(birthweight~AC+BPD+HC+FL+parity+age+DBD,
sigma.fo=~offset(this*AC)++BPD++HC+FL+parity+age+DBD,
data=ultra, family=NO, trace=FALSE))
pp<-prof.term(mod1, min=-0.015, max=0.09, step=.001, criterion="GD")******************************************************************
The Maximum Likelihood estimator is 0.03707175
with a Global Deviance equal to 14696.32
A 95 % Confidence interval is: ( 0.003761827 , 0.07061756 )
****************************************************************** Bayesian Credible interval:
library(bamlss)
b1 <-bamlss(list(mu=birthweight~ AC+BPD+HC+FL+parity+age+DBD,
sigma=~ AC+BPD+HC+FL+parity+age+DBD), data=ultra)summary(b1)
Call:
bamlss(formula = list(mu = birthweight ~ AC + BPD + HC + FL +
parity + age + DBD, sigma = ~AC + BPD + HC + FL + parity +
age + DBD), data = ultra)
---
Family: gaussian
Link function: mu = identity, sigma = log
*---
Formula mu:
---
birthweight ~ AC + BPD + HC + FL + parity + age + DBD
-
Parametric coefficients:
Mean 2.5% 50% 97.5% parameters
(Intercept) -4505.487 -4826.873 -4501.626 -4156.626 -4624.450
AC 154.307 141.231 154.250 166.302 152.828
BPD 99.065 29.798 99.619 168.633 97.275
HC 20.585 -1.756 21.075 41.025 24.521
FL 114.831 45.351 115.996 186.814 120.704
parity1 59.928 20.273 59.569 104.235 59.558
parity2 61.795 4.205 61.137 117.479 61.270
parity3+ 135.651 53.529 134.717 221.268 141.456
age -4.104 -7.347 -3.992 -0.810 -3.727
DBD 28.350 27.089 28.381 29.446 28.581
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.61250 0.08149 0.59965 1
---
Formula sigma:
---
~AC + BPD + HC + FL + parity + age + DBD
-
Parametric coefficients:
Mean 2.5% 50% 97.5% parameters
(Intercept) 5.6489388 4.7257590 5.6197202 6.6375548 5.718
AC 0.0348341 0.0002433 0.0348577 0.0665332 0.037
BPD 0.2491306 0.0557155 0.2528267 0.4436406 0.273
HC -0.0826690 -0.1451788 -0.0832353 -0.0172991 -0.093
FL -0.0997736 -0.2823260 -0.1035470 0.1024356 -0.105
parity1 0.0233884 -0.0824972 0.0226562 0.1279770 0.021
parity2 0.0504966 -0.0988964 0.0513962 0.1984455 0.041
parity3+ -0.0589609 -0.2725091 -0.0565682 0.1735918 -0.085
age -0.0050808 -0.0130429 -0.0048645 0.0031337 -0.005
DBD 0.0063721 0.0032463 0.0064649 0.0092166 0.006
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.7722 0.1712 0.8825 1
---
Sampler summary:
-
DIC = 14736.6 logLik = -7358.441 pd = 19.7155
runtime = 2.301
---
Optimizer summary:
-
AICc = 14737.15 edf = 20 logLik = -7348.161
logPost = -7515.425 nobs = 1038 runtime = 0.023Given the information now we can create the figure. Note that the figure is created with the original results from Boostrapping and MCMC.
y <- c(0.037,0.037,0.039,0.038,0.037,0.034)
CI <- data.frame(
x = c(6:1),
y = y,
yhi = c(0.0703, 0.0813, 0.0875, 0.0786, 0.0701, 0.0665),
ylo = c(0.0037, -0.0072,-0.0076,-0.0052, 0.0037, 0.0002),
labpos = rep(-0.23, 6),
lab = c("Wald", "Robust", "Nonparam. bootstrap", "Bayesian bootstrap",
"Profile likelihood", "Bayesian credible inter."),
rightlabpos = rep(0.1, 6))
CI$rightlab = paste0(CI$y, " (",sprintf("%.4f",CI$ylo), ", ",
sprintf("%.4f",CI$yhi),")")
head(CI,2) x y yhi ylo labpos lab rightlabpos rightlab
1 6 0.037 0.0703 0.0037 -0.23 Wald 0.1 0.037 (0.0037, 0.0703)
2 5 0.037 0.0813 -0.0072 -0.23 Robust 0.1 0.037 (-0.0072, 0.0813)library(ggplot2)
pp <- ggplot(CI, aes(x=x, y=y, ymin=ylo, ymax=yhi)) +
geom_pointrange(shape=16, size=1, position=position_dodge(width=c(0.1))) +
coord_flip() +
geom_hline(aes(yintercept=0), lty=2, lwd=0.25) + # add zero line
scale_x_discrete(breaks=NULL) +
scale_y_continuous(limits = c(-0.25,0.35)) +
theme(legend.position="none") + # no legend
theme_bw() + # take off gray background
ylab(expression(beta[1]^{sigma})) + # the y label
xlab("") +
geom_text(data=CI, aes(x = x, y = labpos, label = lab, hjust=0),size=3) +
geom_text(data=CI, aes(x = x, y = rightlabpos, label = rightlab, hjust=0), size=3)
pp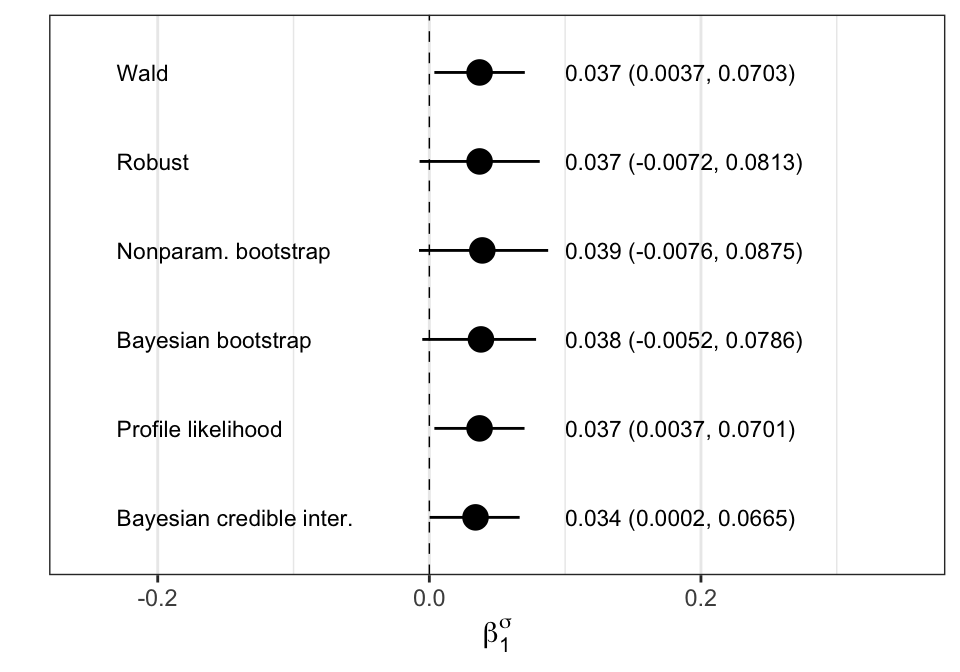
Figure 8.5 (a)
boot_coef_one(B1, 12, dens.fill=gray(.8), rug=F, title="(a)", line.col="gray") +
theme_bw()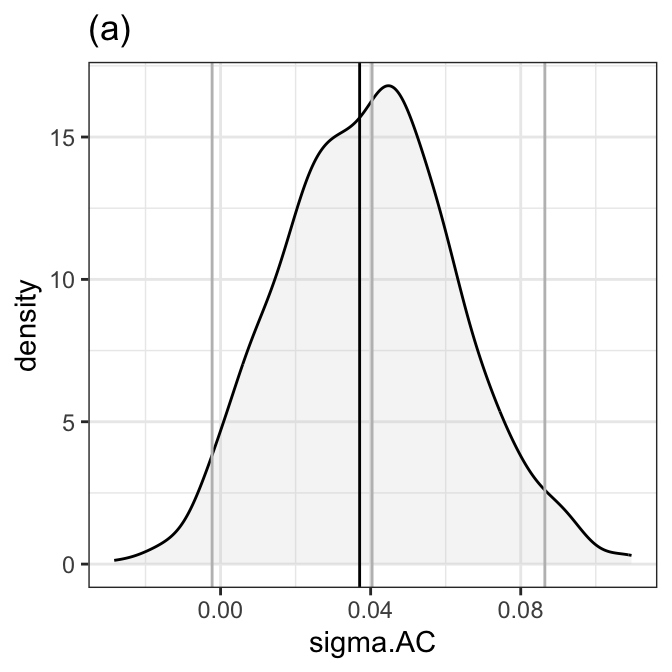
Note that because of re-sampling the figure is sightly different from the book.
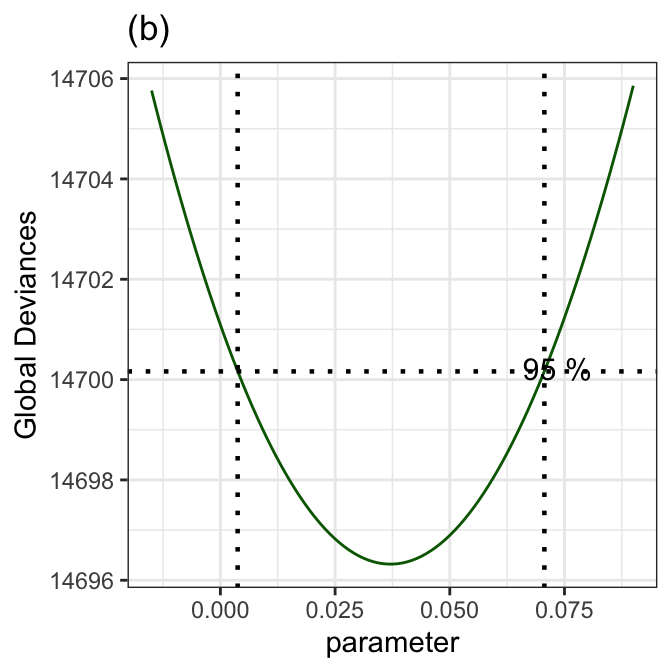
Figure 8.5 (b)
prof_term(mod1, from=-0.015, to=0.09, step=.001, criterion="GD", text.size = 4,
title="(b)") +
theme_bw()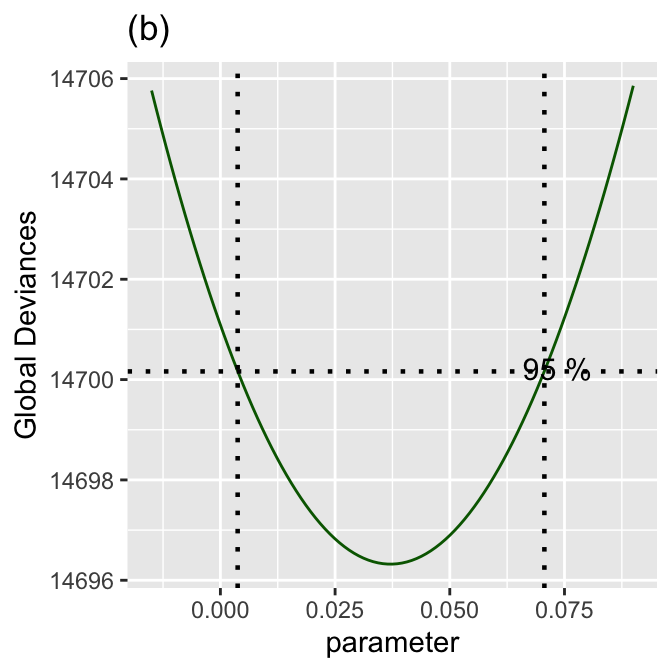
******************************************************************
The Maximum Likelihood estimator is 0.03707175
with a Global Deviance equal to 14696.32
A 95 % Confidence interval is: ( 0.003761827 , 0.07061756 )
****************************************************************** 
Variable selection
Stepwise Procedure (using AIC, k=2)
If you want to see the steps use trace=TRUE.
# AIC
LM3.aic <- stepGAICAll.A(LM1 ,
scope=list(lower=~1, upper=~(AC+BPD+HC+FL+parity+age+DBD)^2),
direction = c("both", "both", "backward"), trace=FALSE)---------------------------------------------------
Start: AIC= 14736.32
birthweight ~ AC + BPD + HC + FL + parity + age + DBD
---------------------------------------------------
Start: AIC= 14695.95
~AC + BPD + HC + FL + parity + age + DBD
---------------------------------------------------
Start: AIC= 14675.63
birthweight ~ AC + BPD + HC + FL + parity + age + DBD + AC:FL +
AC:age + FL:parity + BPD:parity
--------------------------------------------------- summary(LM3.aic)******************************************************************
Family: c("NO", "Normal")
Call: gamlss(formula = birthweight ~ AC + BPD + HC + FL +
parity + age + DBD + AC:FL + AC:age + FL:parity,
sigma.formula = ~AC + BPD + HC + FL + DBD + FL:DBD +
AC:BPD + BPD:FL, family = NO, data = ultra, trace = FALSE)
Fitting method: RS()
------------------------------------------------------------------
Mu link function: identity
Mu Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 44.9118 641.4648 0.070 0.944196
AC -22.8623 23.8056 -0.960 0.337097
BPD 104.2075 32.6388 3.193 0.001453 **
HC 36.2111 10.6080 3.414 0.000667 ***
FL -434.1823 85.8237 -5.059 5.00e-07 ***
parity1 528.8976 195.2468 2.709 0.006865 **
parity2 513.4939 264.8692 1.939 0.052819 .
parity3+ 33.0417 376.9024 0.088 0.930159
age -36.8304 11.6618 -3.158 0.001634 **
DBD 27.9794 0.5367 52.128 < 2e-16 ***
AC:FL 19.5240 2.7076 7.211 1.09e-12 ***
AC:age 1.0606 0.3744 2.833 0.004701 **
FL:parity1 -69.2932 29.2771 -2.367 0.018129 *
FL:parity2 -67.1585 40.1447 -1.673 0.094654 .
FL:parity3+ 13.2815 56.9678 0.233 0.815699
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.866276 3.253685 -0.574 0.56637
AC 0.623347 0.109579 5.689 1.68e-08 ***
BPD 0.919901 0.368466 2.497 0.01270 *
HC -0.068875 0.036390 -1.893 0.05868 .
FL -1.816143 0.835113 -2.175 0.02988 *
DBD 0.054738 0.018480 2.962 0.00313 **
FL:DBD -0.007474 0.002682 -2.787 0.00543 **
AC:BPD -0.066068 0.010206 -6.474 1.49e-10 ***
BPD:FL 0.208372 0.091390 2.280 0.02281 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
No. of observations in the fit: 1038
Degrees of Freedom for the fit: 24
Residual Deg. of Freedom: 1014
at cycle: 5
Global Deviance: 14627.53
AIC: 14675.53
SBC: 14794.21
******************************************************************AIC(nullmodel, LM1, LM2, LM3.aic) df AIC
LM3.aic 24 14675.53
LM2 86 14717.93
LM1 20 14736.32
nullmodel 2 16343.21Stepwise Procedure (using BIC, k=log(n))
If you want to see the steps use trace=TRUE.
# IC
LM3.bic <- stepGAICAll.A(LM1 ,
scope=list(lower=~1, upper=~(AC+BPD+HC+FL+parity+age+DBD)^2),
k=log(881),
direction = c("both", "both", "backward"), trace=FALSE)---------------------------------------------------
Start: AIC= 14831.94
birthweight ~ AC + BPD + HC + FL + parity + age + DBD
---------------------------------------------------
Start: AIC= 14795.26
~AC + BPD + HC + FL + parity + age + DBD
---------------------------------------------------
Start: AIC= 14756.6
birthweight ~ AC + BPD + HC + FL + DBD + AC:FL
--------------------------------------------------- summary(LM3.bic)******************************************************************
Family: c("NO", "Normal")
Call: gamlss(formula = birthweight ~ AC + BPD + FL + DBD +
AC:FL, sigma.formula = ~BPD + DBD + BPD:DBD, family = NO,
data = ultra, trace = FALSE)
Fitting method: RS()
------------------------------------------------------------------
Mu link function: identity
Mu Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1051.8543 616.2561 -1.707 0.0882 .
AC 32.2965 23.2092 1.392 0.1644
BPD 169.9712 26.0263 6.531 1.03e-10 ***
FL -415.3691 96.7911 -4.291 1.94e-05 ***
DBD 28.2321 0.5683 49.678 < 2e-16 ***
AC:FL 18.1250 3.1988 5.666 1.89e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.754846 0.567981 6.611 6.13e-11 ***
BPD 0.194815 0.061262 3.180 0.00152 **
DBD 0.036021 0.012835 2.806 0.00510 **
BPD:DBD -0.003411 0.001302 -2.619 0.00894 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
No. of observations in the fit: 1038
Degrees of Freedom for the fit: 10
Residual Deg. of Freedom: 1028
at cycle: 4
Global Deviance: 14688.43
AIC: 14708.43
SBC: 14757.88
******************************************************************GAIC(nullmodel, LM1, LM2, LM3.aic, LM3.bic) df AIC
LM3.aic 24 14675.53
LM3.bic 10 14708.43
LM2 86 14717.93
LM1 20 14736.32
nullmodel 2 16343.21Stepwise Procedure (using k=4)
If you want to see the steps use trace=TRUE.
# BIC
LM3.k4 <- stepGAICAll.A(LM1 ,
scope=list(lower=~1, upper=~(AC+BPD+HC+FL+parity+age+DBD)^2),
k=4, direction = c("both", "both", "backward"), trace=FALSE)---------------------------------------------------
Start: AIC= 14776.32
birthweight ~ AC + BPD + HC + FL + parity + age + DBD
---------------------------------------------------
Start: AIC= 14740.76
~AC + BPD + HC + FL + parity + age + DBD
---------------------------------------------------
Start: AIC= 14717.45
birthweight ~ AC + BPD + HC + FL + parity + age + DBD + AC:FL +
AC:age
--------------------------------------------------- summary(LM3.bic)******************************************************************
Family: c("NO", "Normal")
Call: gamlss(formula = birthweight ~ AC + BPD + FL + DBD +
AC:FL, sigma.formula = ~BPD + DBD + BPD:DBD, family = NO,
data = ultra, trace = FALSE)
Fitting method: RS()
------------------------------------------------------------------
Mu link function: identity
Mu Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1051.8543 616.2561 -1.707 0.0882 .
AC 32.2965 23.2092 1.392 0.1644
BPD 169.9712 26.0263 6.531 1.03e-10 ***
FL -415.3691 96.7911 -4.291 1.94e-05 ***
DBD 28.2321 0.5683 49.678 < 2e-16 ***
AC:FL 18.1250 3.1988 5.666 1.89e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.754846 0.567981 6.611 6.13e-11 ***
BPD 0.194815 0.061262 3.180 0.00152 **
DBD 0.036021 0.012835 2.806 0.00510 **
BPD:DBD -0.003411 0.001302 -2.619 0.00894 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
------------------------------------------------------------------
No. of observations in the fit: 1038
Degrees of Freedom for the fit: 10
Residual Deg. of Freedom: 1028
at cycle: 4
Global Deviance: 14688.43
AIC: 14708.43
SBC: 14757.88
******************************************************************GAIC(nullmodel, LM1, LM2, LM3.aic, LM3.bic, LM3.k4) df AIC
LM3.aic 24 14675.53
LM3.k4 20 14677.45
LM3.bic 10 14708.43
LM2 86 14717.93
LM1 20 14736.32
nullmodel 2 16343.21Shrinking procedures
LASSO
We create a design matrix with all main effects and first order interactions and save the response and the design matrix to a data.frame called ultra1.
library(gamlss.lasso)
X <- model.matrix(~(AC+BPD+HC+FL+parity+age+DBD)^2, data=ultra)
dim(X)[1] 1038 43ultra1 <- data.frame(birthweight=ultra$birthweight, X[,-1])
names(ultra1) [1] "birthweight" "AC" "BPD" "HC" "FL"
[6] "parity1" "parity2" "parity3." "age" "DBD"
[11] "AC.BPD" "AC.HC" "AC.FL" "AC.parity1" "AC.parity2"
[16] "AC.parity3." "AC.age" "AC.DBD" "BPD.HC" "BPD.FL"
[21] "BPD.parity1" "BPD.parity2" "BPD.parity3." "BPD.age" "BPD.DBD"
[26] "HC.FL" "HC.parity1" "HC.parity2" "HC.parity3." "HC.age"
[31] "HC.DBD" "FL.parity1" "FL.parity2" "FL.parity3." "FL.age"
[36] "FL.DBD" "parity1.age" "parity2.age" "parity3..age" "parity1.DBD"
[41] "parity2.DBD" "parity3..DBD" "age.DBD" dim(ultra1)[1] 1038 43any(is.na(X))[1] FALSEThe following output is to check whether the linear model with interactions is the same as the one fitted by the scaled x-variables data.
LM22 <- gamlss(birthweight~scale(X[,-1]), data=ultra1,
sigma.fo=~scale(X[,-1]),
family=NO, bf.cyc=1, n.cyc=50, trace=F)
AIC(LM2, LM22, k=0) df AIC
LM2 86 14545.93
LM22 86 14545.93The models LM2 and LM22 have identical deviances as we would expect, but with a completely different set of fitted coefficients. That is because the x’s are on a different scale. You can verify this by plotting the two set of coefficients using:
plot(coef(LM2)~coef(LM22))The package gamlss.lasso can be used to fit LASSO models within GAMLSS. The default setting of the LASSO is adaptive lasso with BIC tuning. Note that the argument method has two options, information criterion, “IC”, and cross validation, “CV”, and that the argument method=IC has options c("BIC", "HQC", "AIC"). To start with we estimate only the \(\mu\) model (NOT in the book) using the default setting: adaptive lasso with BIC:
LM41.ad.lasso.bic <- gamlss(birthweight~gnet(x.vars= names(ultra1)[-c(1)],method = "IC", ICpen="BIC"),
data=ultra1, family=NO, bf.cyc=1)GAMLSS-RS iteration 1: Global Deviance = 14816.5
GAMLSS-RS iteration 2: Global Deviance = 14816.5 Note that the same model can be fitted using with just
M4m0 <- gamlss(birthweight~gnet(x.vars=names(ultra1)[-c(1)]), data=ultra1, family=NO, bf.cyc=1)GAMLSS-RS iteration 1: Global Deviance = 14816.5
GAMLSS-RS iteration 2: Global Deviance = 14816.5 Here we fit the model used in the book which models both \(\mu\) and \(\sigma\). Note that we import our own version of the gnet() function and also some additional functions which are not in the package gamlss.lasso yet.
source("R/glmnet_gamlss.R")
source("R/create_data.R")
LM4.ad.lasso.bic <- gamlss(birthweight~gnet(x.vars=names(ultra1)[-1]),
sigma.fo=~gnet(x.vars=names(ultra1)[-1]), data=ultra1,
family=NO, i.control = glim.control(cyc=1, bf.cyc=1))GAMLSS-RS iteration 1: Global Deviance = 14949.13
GAMLSS-RS iteration 2: Global Deviance = 14695.82
GAMLSS-RS iteration 3: Global Deviance = 14658.48
GAMLSS-RS iteration 4: Global Deviance = 14669.94
GAMLSS-RS iteration 5: Global Deviance = 14672
GAMLSS-RS iteration 6: Global Deviance = 14681.55
GAMLSS-RS iteration 7: Global Deviance = 14685.01
GAMLSS-RS iteration 8: Global Deviance = 14685.89
GAMLSS-RS iteration 9: Global Deviance = 14685.89 Here we display the nonzero coefficients for the \(\mu\) and \(\sigma\) models.
gnet_terms(LM4.ad.lasso.bic, parameter="mu") AC BPD FL parity1 parity3. age
156.239204 136.291348 146.203141 54.628206 104.694214 -3.222064
DBD BPD.parity2
28.511972 3.820405 gnet_terms(LM4.ad.lasso.bic, parameter="sigma") AC BPD HC FL parity1
2.814530e-02 1.730529e-01 -4.077744e-02 -1.205020e-01 1.439268e-01
parity2 parity3. age DBD BPD.parity3.
1.428673e+00 -3.992279e+00 -2.331670e-03 5.722929e-03 4.139289e-01
HC.parity1 HC.parity2 FL.parity3. FL.DBD parity1.DBD
-8.155753e-03 -4.563783e-02 -5.189657e-04 -2.503784e-04 4.240641e-03
parity2.DBD parity3..DBD
4.930397e-05 1.071039e-02 Other additional functions are; gnet_path(), gnet_terms(),gnet_coef(), and gnet_df(). For example to get the path of the fit for \(\mu\) use:
gnet_path(LM4.ad.lasso.bic,parameter="mu" )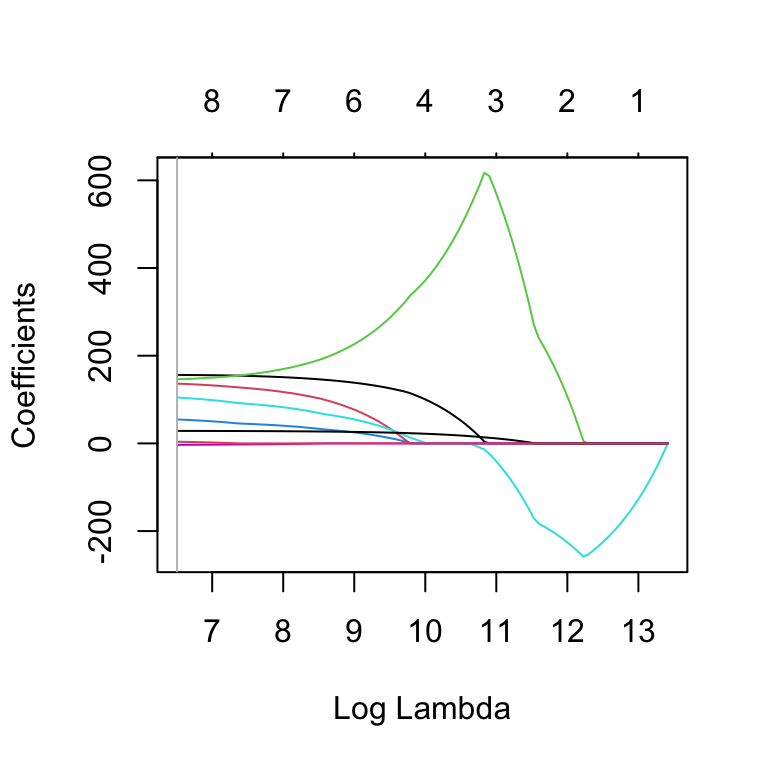
PCR
The fit needs the package gamlss.foreach:
library(gamlss.foreach)
registerDoParallel(cores = 8)
LM5.pcr <- gamlss(birthweight~pcr(x.vars = names(ultra1)[-c(1)]),
sigma.fo= ~ pcr(x.vars=names(ultra1)[-c(1)]),
data=ultra1)GAMLSS-RS iteration 1: Global Deviance = 14675.29
GAMLSS-RS iteration 2: Global Deviance = 14674.97
GAMLSS-RS iteration 3: Global Deviance = 14674.98
GAMLSS-RS iteration 4: Global Deviance = 14674.99
GAMLSS-RS iteration 5: Global Deviance = 14674.99 plot(getSmo(LM5.pcr, "mu"))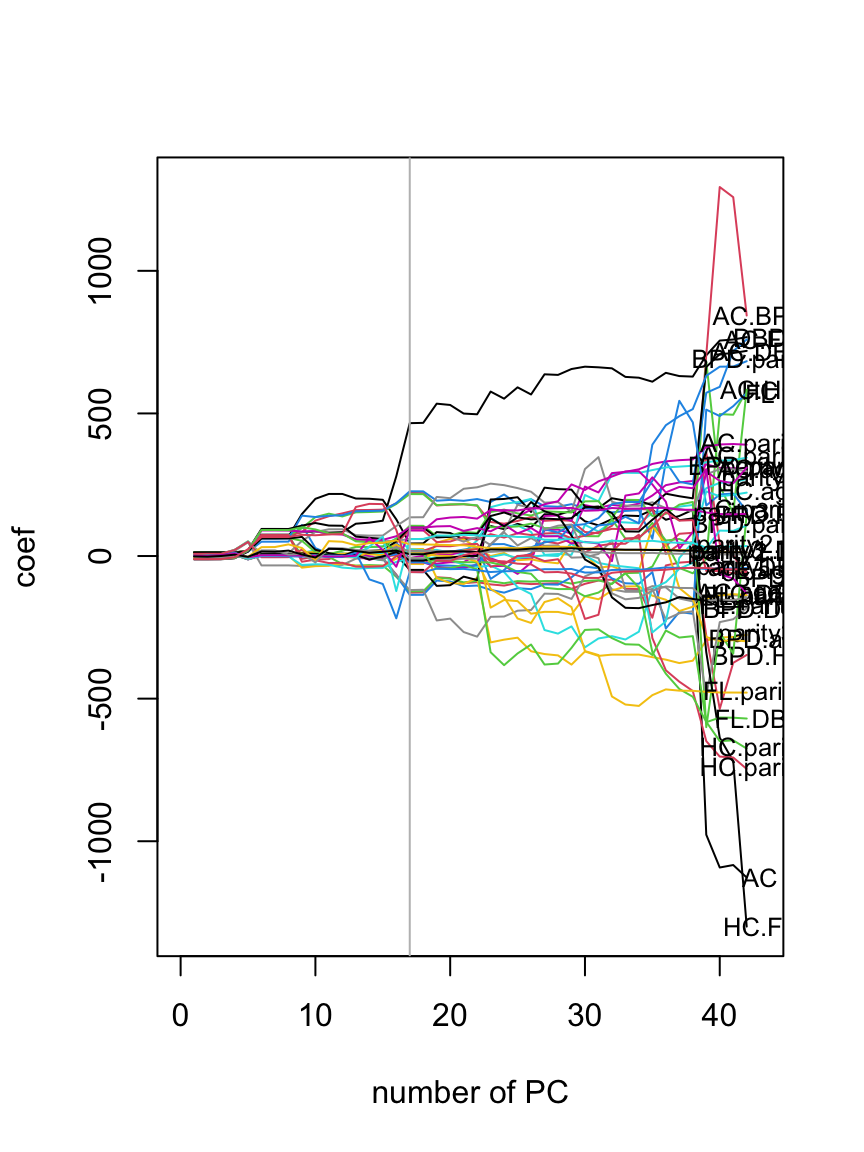
getSmo(LM5.pcr)$pc[1] 17plot(getSmo(LM5.pcr, "sigma"))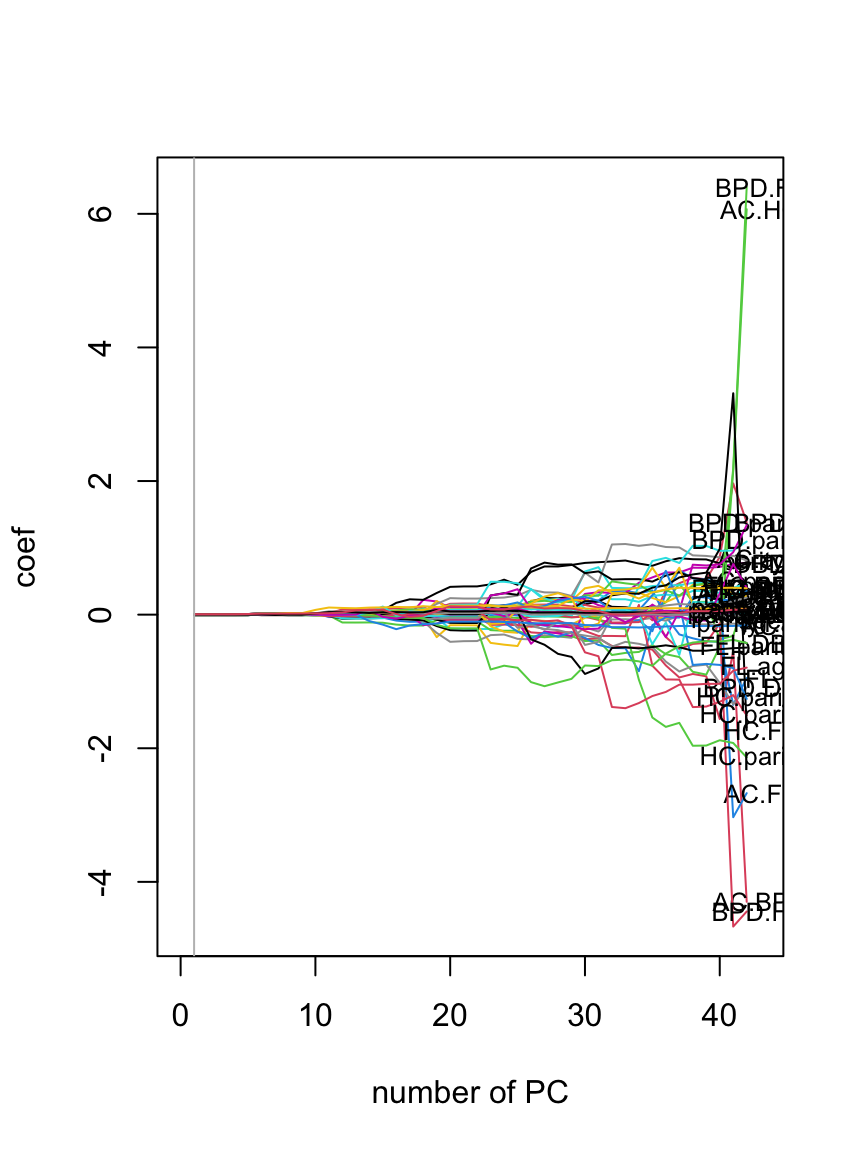
getSmo(LM5.pcr, "sigma")$pc[1] 1Table 8.5
GAIC.table(nullmodel, LM1, LM2, LM3.aic, LM3.bic, LM4.ad.lasso.bic, LM5.pcr)minimum GAIC(k= 2 ) model: LM3.aic
minimum GAIC(k= 3.84 ) model: LM3.aic
minimum GAIC(k= 6.95 ) model: LM3.bic df k=2 k=3.84 k=6.95
nullmodel 2 16343.21 16346.89 16353.11
LM1 20 14736.32 14773.12 14835.32
LM2 86 14717.93 14876.17 15143.63
LM3.aic 24 14675.53 14719.69 14794.33
LM3.bic 10 14708.43 14726.83 14757.93
LM4.ad.lasso.bic 27 14739.89 14789.57 14873.54
LM5.pcr 20 14714.99 14751.79 14813.99Figure 8.6 (a)
model_wp(LM1,LM2,LM3.aic, LM3.bic, LM4.ad.lasso.bic, LM5.pcr, title="(a)") +
theme_bw(base_size = 15) +
theme(legend.position = "none")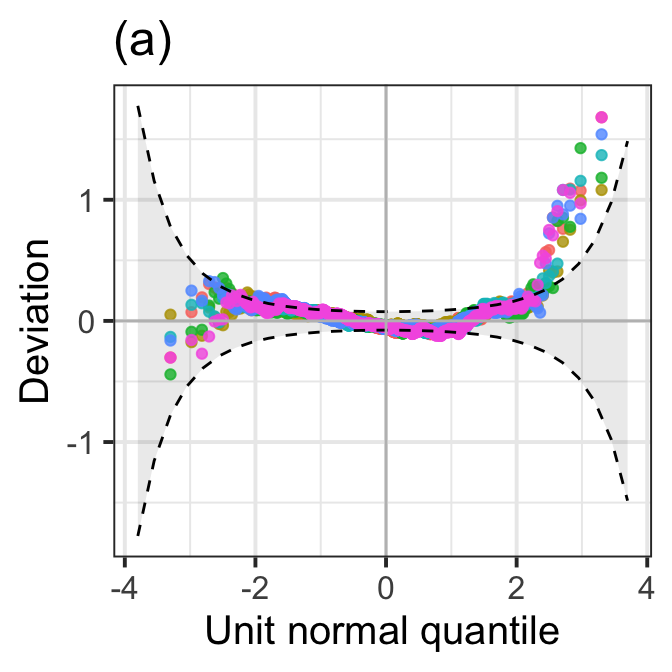
Figure 8.6 (b)
moment_bucket(LM1,LM2,LM3.aic, LM3.bic, LM4.ad.lasso.bic,LM5.pcr,
text_to_show = c("1","2","3a","3b","4","5"), cex_text = 6) +
ggtitle("(b)") +
ylab("moment excess kurtosis") +
xlab("moment skewness") +
theme_bw(base_size = 15) +
theme(legend.position = "none")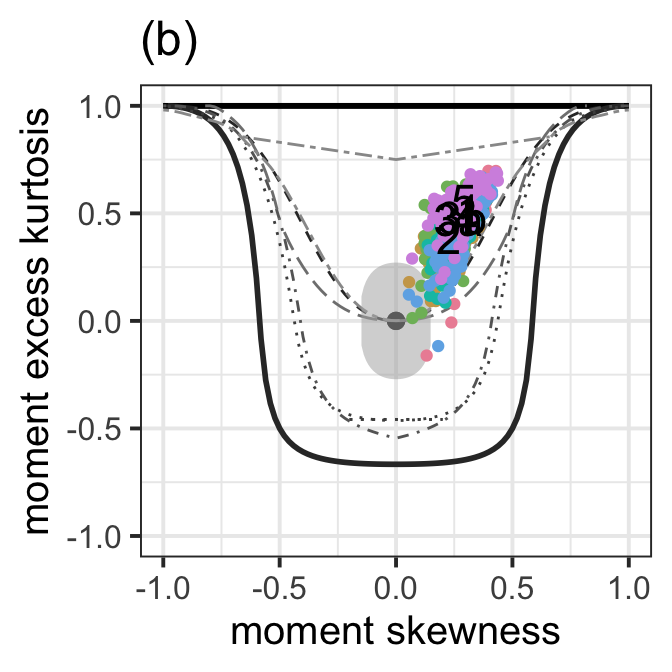
Figure 8.7
TLM1 <- chooseDist(LM3.bic, parallel="snow", ncpus = 8)minimum GAIC(k= 2 ) family: JSU
minimum GAIC(k= 3.84 ) family: JSU
minimum GAIC(k= 6.95 ) family: JSU model_GAIC_lollipop(TLM1, title="(a) AIC for fitted distributions",
col.point=gray(.3), col="gray", order.val="TRUE")+
theme_bw(base_size = 15)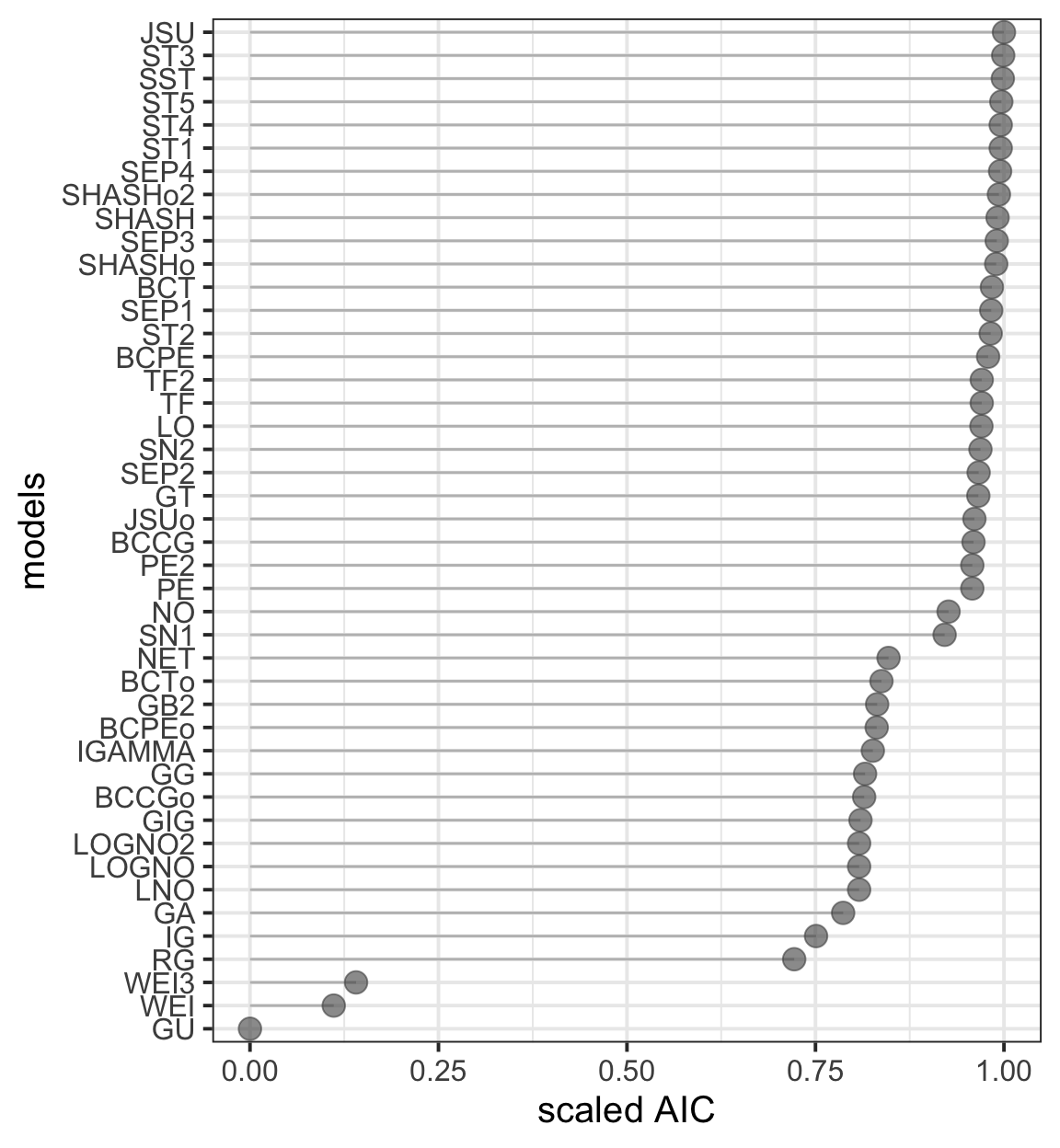
getOrder(TLM1)[1:5]GAIG with k= 2 JSU ST3 SST ST5 ST1
14681.07 14681.45 14681.62 14682.36 14682.66 getOrder(TLM1,2)[1:5]GAIG with k= 3.84 JSU ST3 SST ST5 ST1
14703.15 14703.53 14703.70 14704.44 14704.74 getOrder(TLM1,3)[1:5]GAIG with k= 6.95 JSU ST3 SST LO ST5
14740.47 14740.85 14741.02 14741.72 14741.76 Figure 8.8
LM7.jsu <- update(LM3.bic, family=JSU)
resid_wp(LM7.jsu, points_col=gray(.4),
title=NULL)+
theme_bw(base_size = 15) 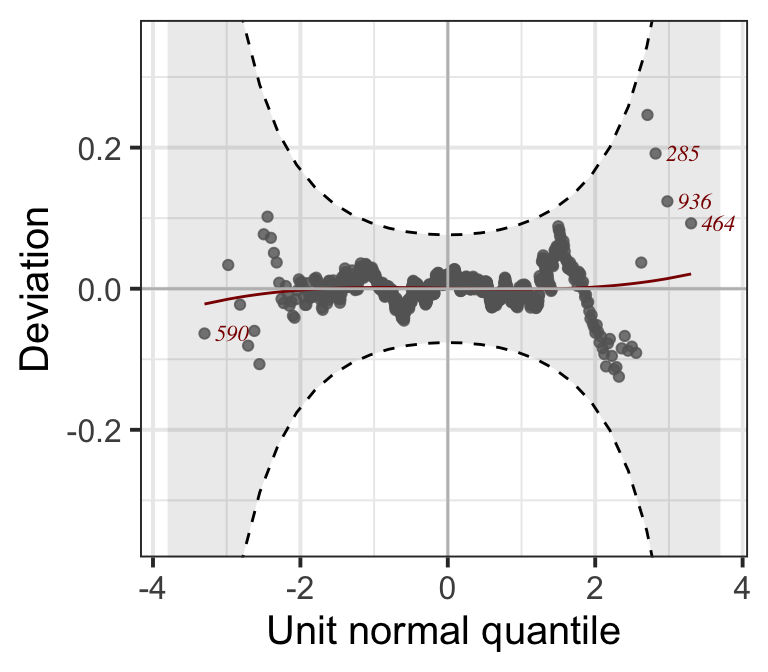
Figure 8.9 (a)
Select model using AIC:
null.jsu <- gamlss(birthweight ~ 1, family = JSU, data = ultra, trace = FALSE)
LM7.jsu.aic <- stepGAICAll.A(null.jsu ,
scope=list(lower=~1, upper=~(AC+BPD+HC+FL+parity+age+DBD)^2),
trace=FALSE, k=2, parallel="snow", ncpus = 8)---------------------------------------------------
Start: AIC= 16323.64
birthweight ~ 1
---------------------------------------------------
Start: AIC= 14685.11
~1
---------------------------------------------------
Start: AIC= 14654.57
~1
---------------------------------------------------
Start: AIC= 14646.01
~1
---------------------------------------------------
Start: AIC= 14646.01
~AC + DBD
---------------------------------------------------
Start: AIC= 14646.01
~DBD + AC + FL + age + DBD:AC + DBD:FL
---------------------------------------------------
Start: AIC= 14644.73
birthweight ~ AC + DBD + HC + FL + parity + age + BPD + AC:HC +
FL:parity + AC:age + AC:BPD
--------------------------------------------------- LM7.jsu.aic
Family: c("JSU", "Johnson SU")
Fitting method: RS()
Call: gamlss(formula = birthweight ~ AC + DBD + HC + FL +
parity + age + BPD + FL:parity + AC:age + AC:BPD,
sigma.formula = ~DBD + AC + FL + DBD:FL, nu.formula = ~AC +
DBD, tau.formula = ~1, family = JSU, data = ultra, trace = FALSE)
Mu Coefficients:
(Intercept) AC DBD HC FL parity1
566.0558 -41.0944 27.9746 38.2969 205.8472 550.2151
parity2 parity3+ age BPD FL:parity1 FL:parity2
489.9364 157.2908 -33.4186 -464.0376 -71.9149 -64.4846
FL:parity3+ AC:age AC:BPD
-0.3978 0.9550 17.3606
Sigma Coefficients:
(Intercept) DBD AC FL DBD:FL
4.641916 0.029291 0.039539 -0.061687 -0.003644
Nu Coefficients:
(Intercept) AC DBD
15.39684 -0.40890 -0.05691
Tau Coefficients:
(Intercept)
0.9442
Degrees of Freedom for the fit: 24 Residual Deg. of Freedom 1014
Global Deviance: 14594.8
AIC: 14642.8
SBC: 14761.5 Select model using BIC:
LM7.jsu.bic <- stepGAICAll.A(null.jsu,
scope=list(lower=~1, upper=~(AC+BPD+HC+FL+parity+age+DBD)^2),
k=log(1038), parallel="snow", ncpus = 8, trace=FALSE)---------------------------------------------------
Start: AIC= 16343.42
birthweight ~ 1
---------------------------------------------------
Start: AIC= 14755.61
~1
---------------------------------------------------
Start: AIC= 14733.46
~1
---------------------------------------------------
Start: AIC= 14733.46
~1
---------------------------------------------------
Start: AIC= 14733.46
~1
---------------------------------------------------
Start: AIC= 14733.46
~DBD
---------------------------------------------------
Start: AIC= 14733.46
birthweight ~ AC + DBD + HC + FL + AC:HC
--------------------------------------------------- LM7.jsu.bic
Family: c("JSU", "Johnson SU")
Fitting method: RS()
Call: gamlss(formula = birthweight ~ AC + DBD + HC + FL +
AC:HC, sigma.formula = ~DBD, family = JSU, data = ultra,
trace = FALSE, nu.formula = ~1, tau.formula = ~1)
Mu Coefficients:
(Intercept) AC DBD HC FL AC:HC
-678.286 11.294 28.404 -84.907 152.750 4.508
Sigma Coefficients:
(Intercept) DBD
5.490173 0.006265
Nu Coefficients:
(Intercept)
0.688
Tau Coefficients:
(Intercept)
0.8143
Degrees of Freedom for the fit: 10 Residual Deg. of Freedom 1028
Global Deviance: 14664
AIC: 14684
SBC: 14733.5 Now the first plot:
model_wp(LM7.jsu.aic,LM7.jsu.bic, title="(a)") +
theme_bw(base_size = 15) +
theme(legend.position = "none")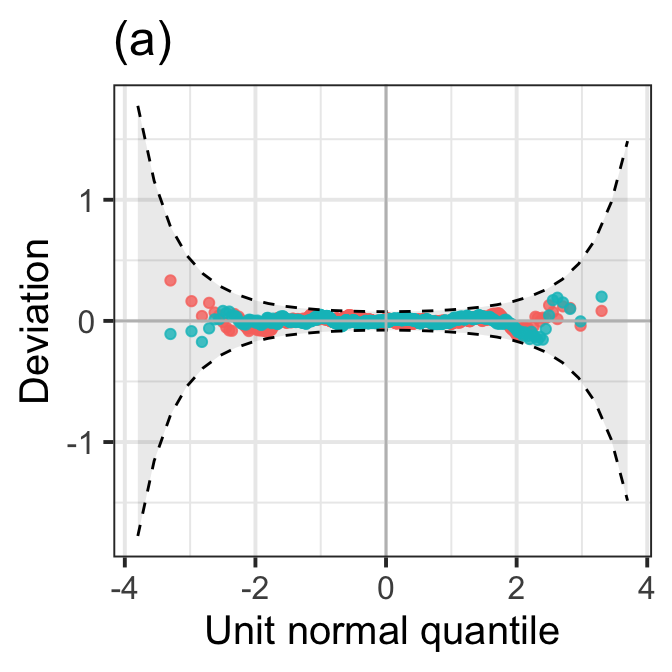
The second plot;
moment_bucket(LM7.jsu.aic,LM7.jsu.bic,
text_to_show = c("1","2"), cex_text = 7 ) + ggtitle("(b)")+
ylab("moment excess kurtosis")+xlab("moment skewness")+
theme_bw(base_size = 15)+
theme(legend.position = "none")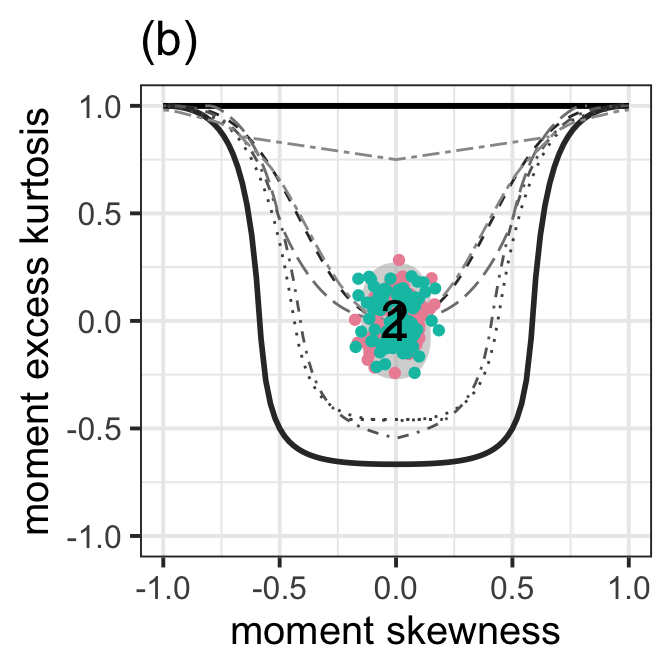
Figure 8.10
fitted_terms(LM7.jsu.bic, term.col="black", col.ribbon = gray(.3))+
theme_bw(base_size = 30)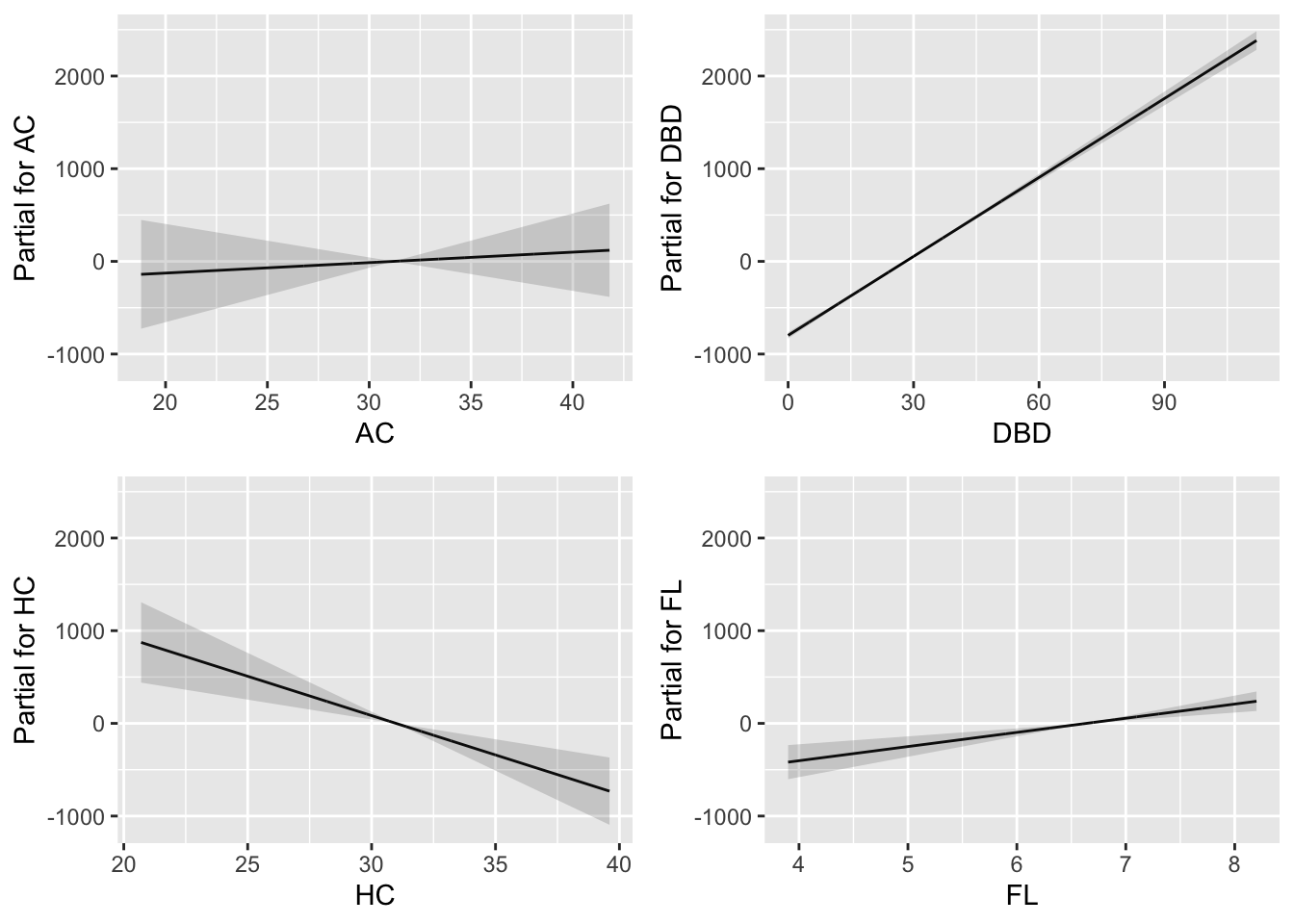
NULLFigure 8.11
pe_param_grid(LM7.jsu.bic, col="black",
terms=list("AC", "DBD", "HC", "FL", c("AC", "HC")))+
theme_bw(base_size = 30)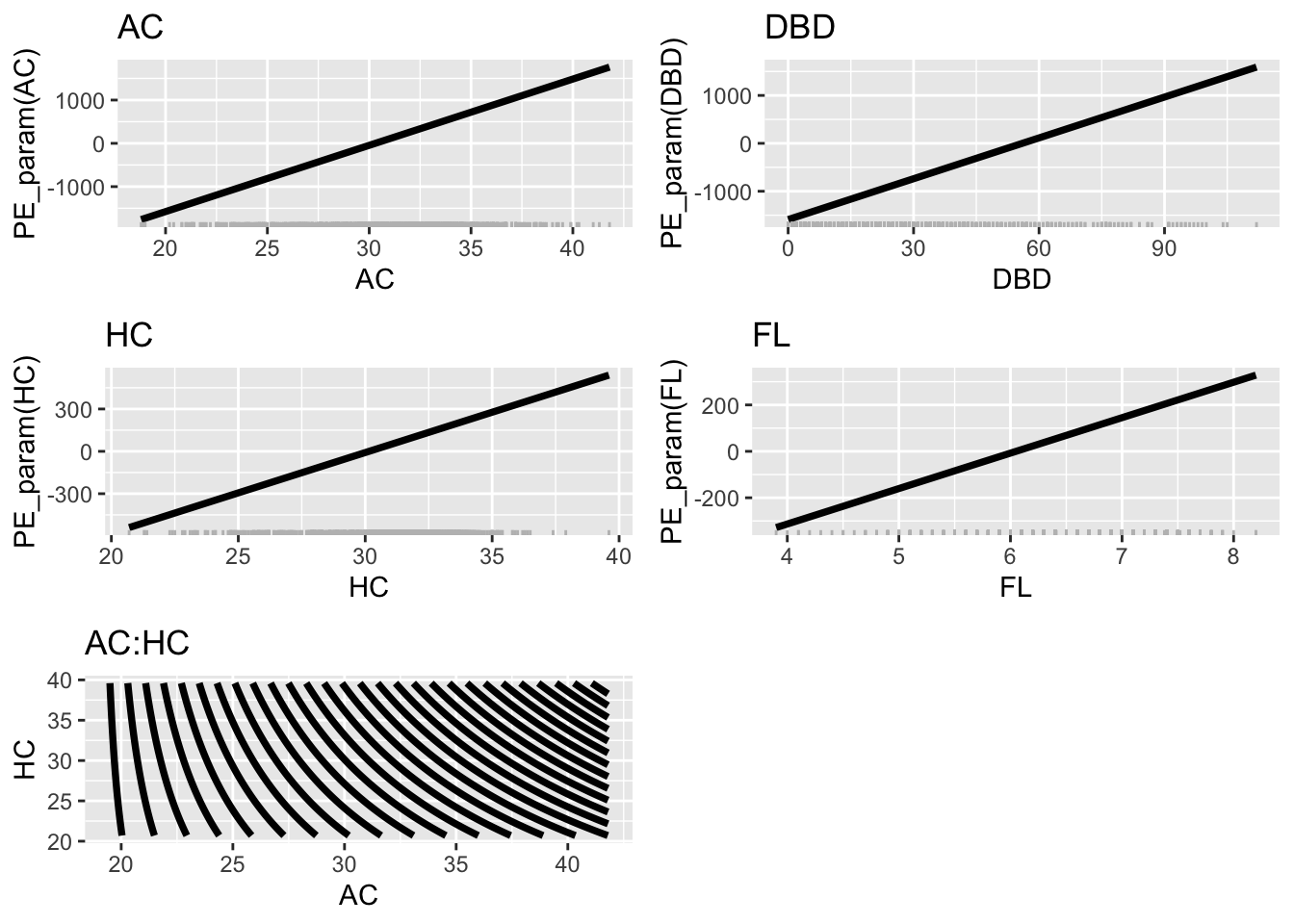
NULLFigure 8.12
library(gamlss.add)
LM7.jsu.bic_smo_i = gamlss(birthweight ~ pb(AC)+ pb(DBD) + pb(HC) + pb(FL) + ga(~s(AC,HC)),
sigma.formula = ~DBD,
nu.formula = ~1,
tau.formula = ~1,
family = JSU, data = ultra, bf.cyc=1)GAMLSS-RS iteration 1: Global Deviance = 14711.84
GAMLSS-RS iteration 2: Global Deviance = 14687.84
GAMLSS-RS iteration 3: Global Deviance = 14666.85
GAMLSS-RS iteration 4: Global Deviance = 14656.35
GAMLSS-RS iteration 5: Global Deviance = 14653.5
GAMLSS-RS iteration 6: Global Deviance = 14652.99
GAMLSS-RS iteration 7: Global Deviance = 14652.93
GAMLSS-RS iteration 8: Global Deviance = 14652.94
GAMLSS-RS iteration 9: Global Deviance = 14652.95
GAMLSS-RS iteration 10: Global Deviance = 14652.96
GAMLSS-RS iteration 11: Global Deviance = 14652.96
GAMLSS-RS iteration 12: Global Deviance = 14652.96
GAMLSS-RS iteration 13: Global Deviance = 14652.96 library(gamlss.add)
pe_param_grid(LM7.jsu.bic_smo_i, col="black",
terms=list( "AC","DBD", "HC", "FL", c("AC", "HC")))+
theme_bw(base_size = 30)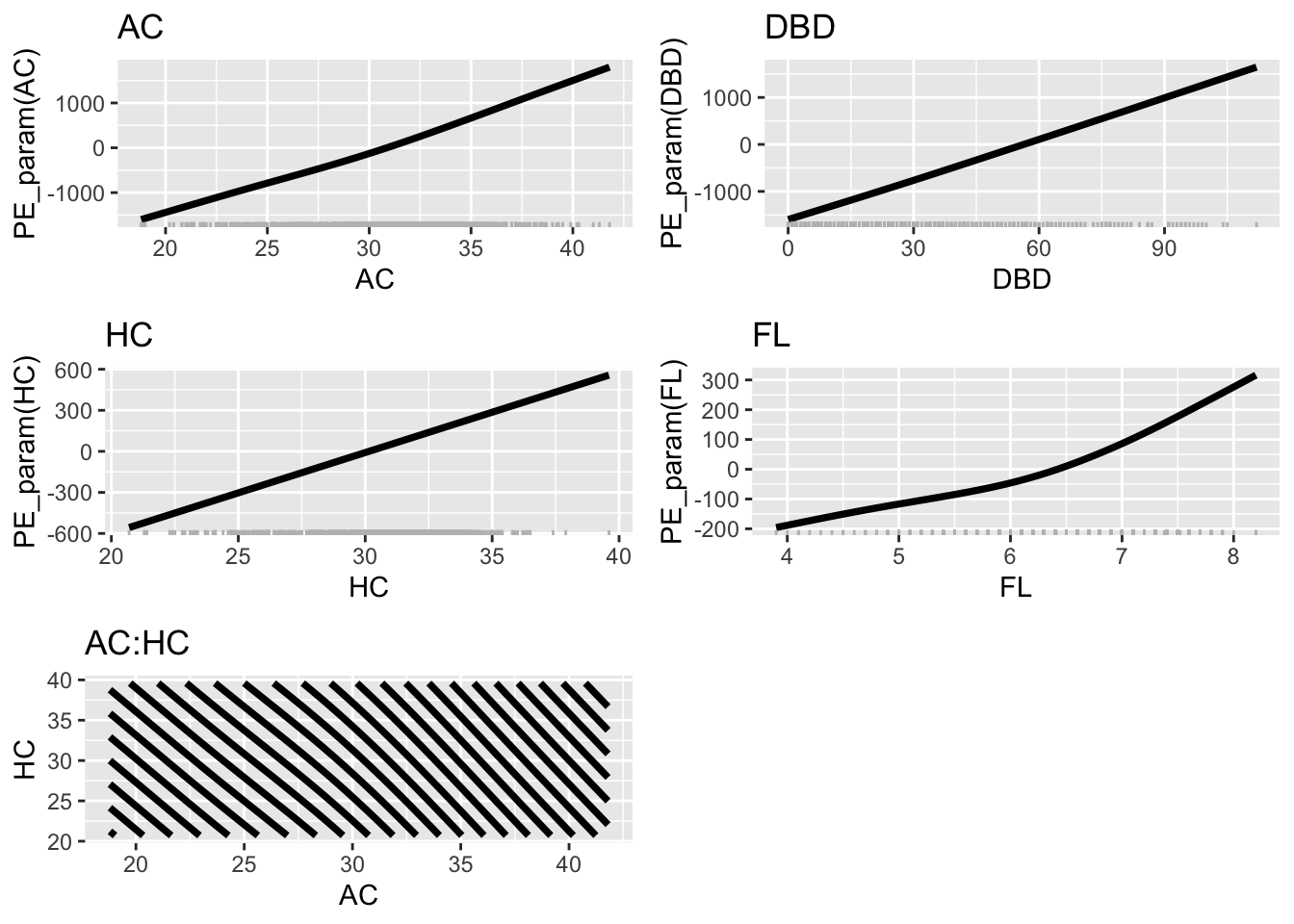
new prediction
new prediction
new prediction
new prediction
new prediction NULLFigure 8.13 (a)
pp <- getPEF(LM7.jsu.bic_smo_i, "FL")new prediction FL <- seq(3.9,8.2, 0.01)
da =data.frame(FL=FL, MU=pp(FL), dMU =pp(FL,deriv=1))
ggplot(da, aes(x=FL, y=MU))+ggtitle("(a)")+
geom_line()+theme_bw(base_size = 15)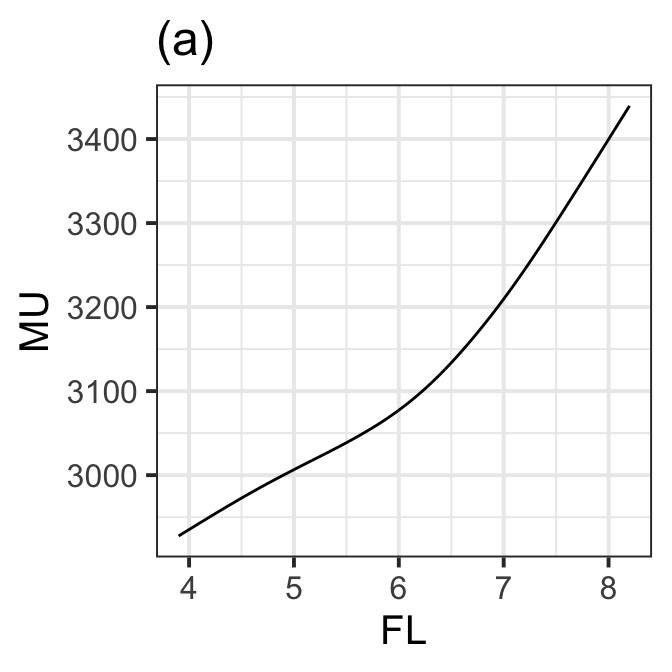
Figure 8.13 (b)
ggplot(da, aes(x=FL, y=dMU))+ggtitle("(b)")+
geom_line()+
theme_bw(base_size = 15)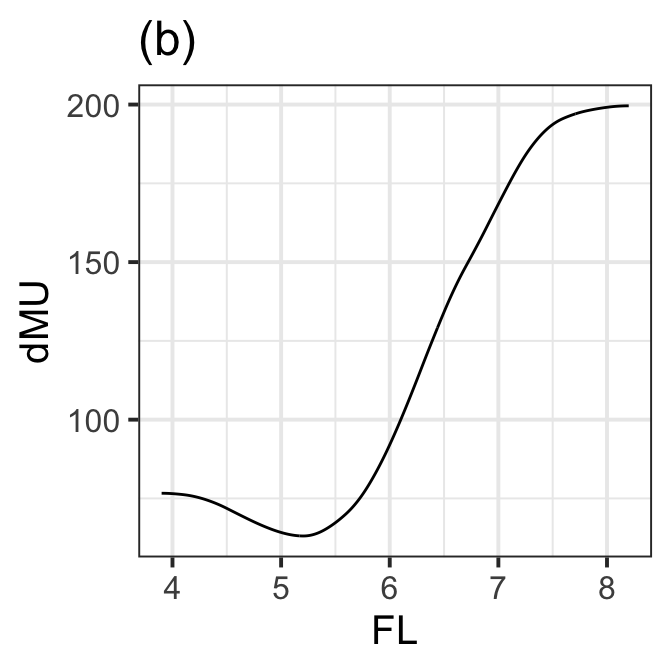
Figure 8.14 (a)
gamlss.ggplots:::pe_moment(LM7.jsu.aic,"AC", title="(a) ", col="black") +
theme_bw(base_size = 15)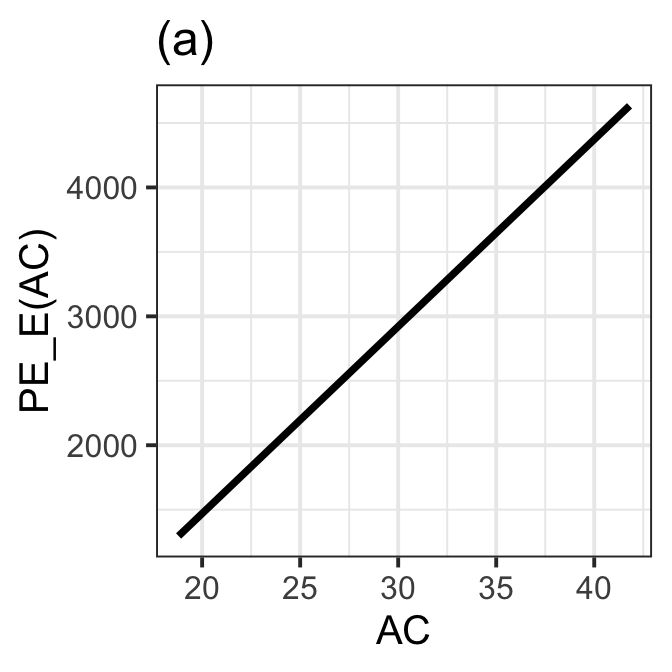
Figure 8.14 (b)
gamlss.ggplots:::pe_moment(LM7.jsu.aic, "AC", moment="sd", title="(b)") +
theme_bw(base_size = 15)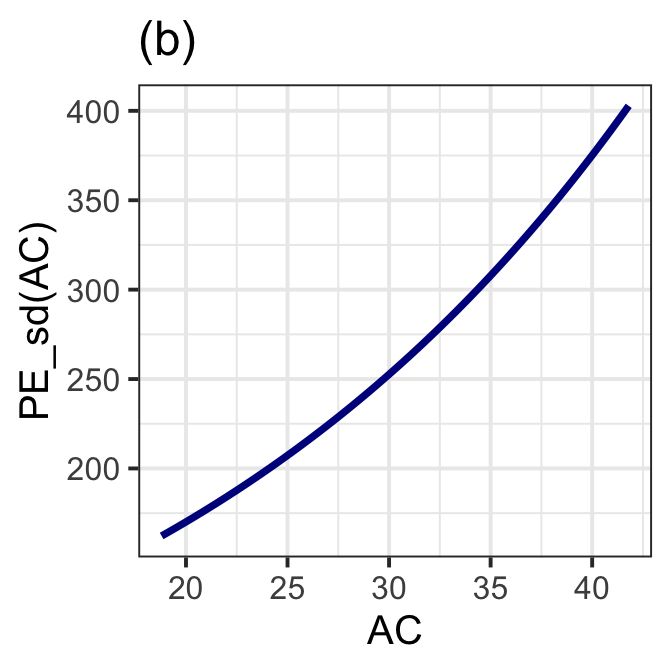
Figure 8.14 (c)
gamlss.ggplots:::pe_moment(LM7.jsu.aic,"parity", title="(c)") +
theme_bw(base_size = 15)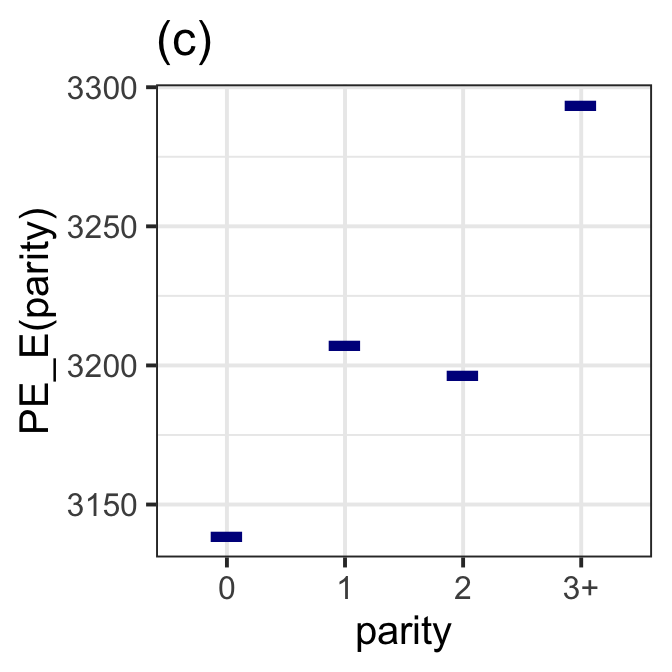
Figure 8.14 (d)
gamlss.ggplots:::pe_moment(LM7.jsu.aic,"parity", moment="var", title="(d)") +
theme_bw(base_size = 15)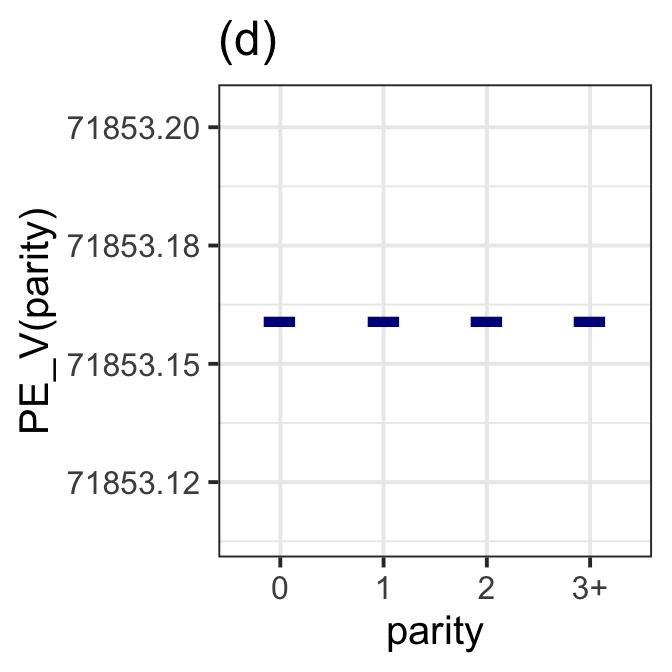
Figure 8.15
library(grid)
source("R/pe_1_quantile.R")
source("R/pe_quantile_grid.R")
source("R/pe_2_quantile.R")
pe_quantile_grid(LM7.jsu.aic,c("DBD", "AC", "HC", "parity", "FL"), legend=FALSE) +
theme_bw(base_size = 20)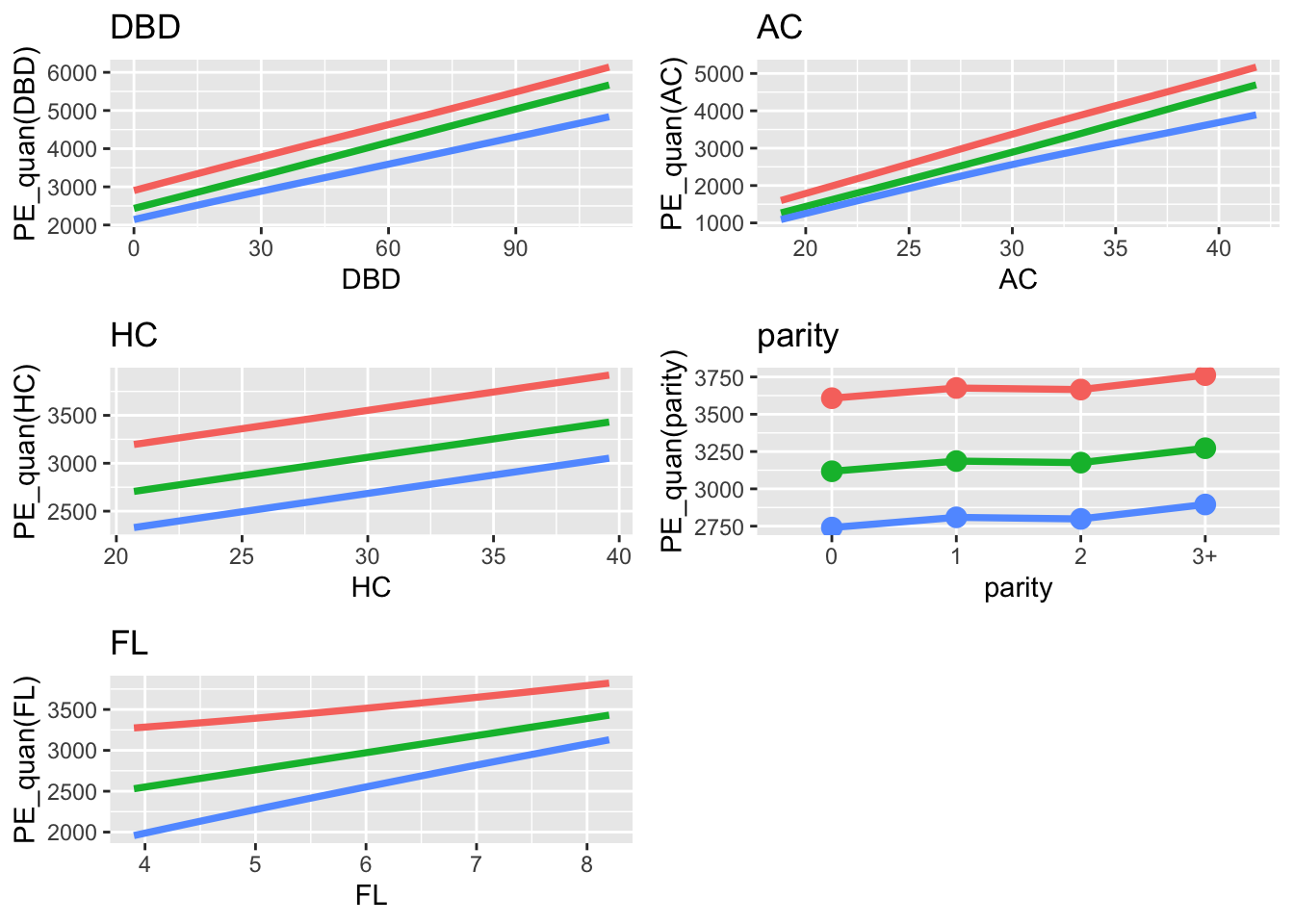
NULLFigure 8.16
pe_2_quantile(LM7.jsu.bic,c("AC", "HC"), title="") +
theme_bw(base_size = 15) 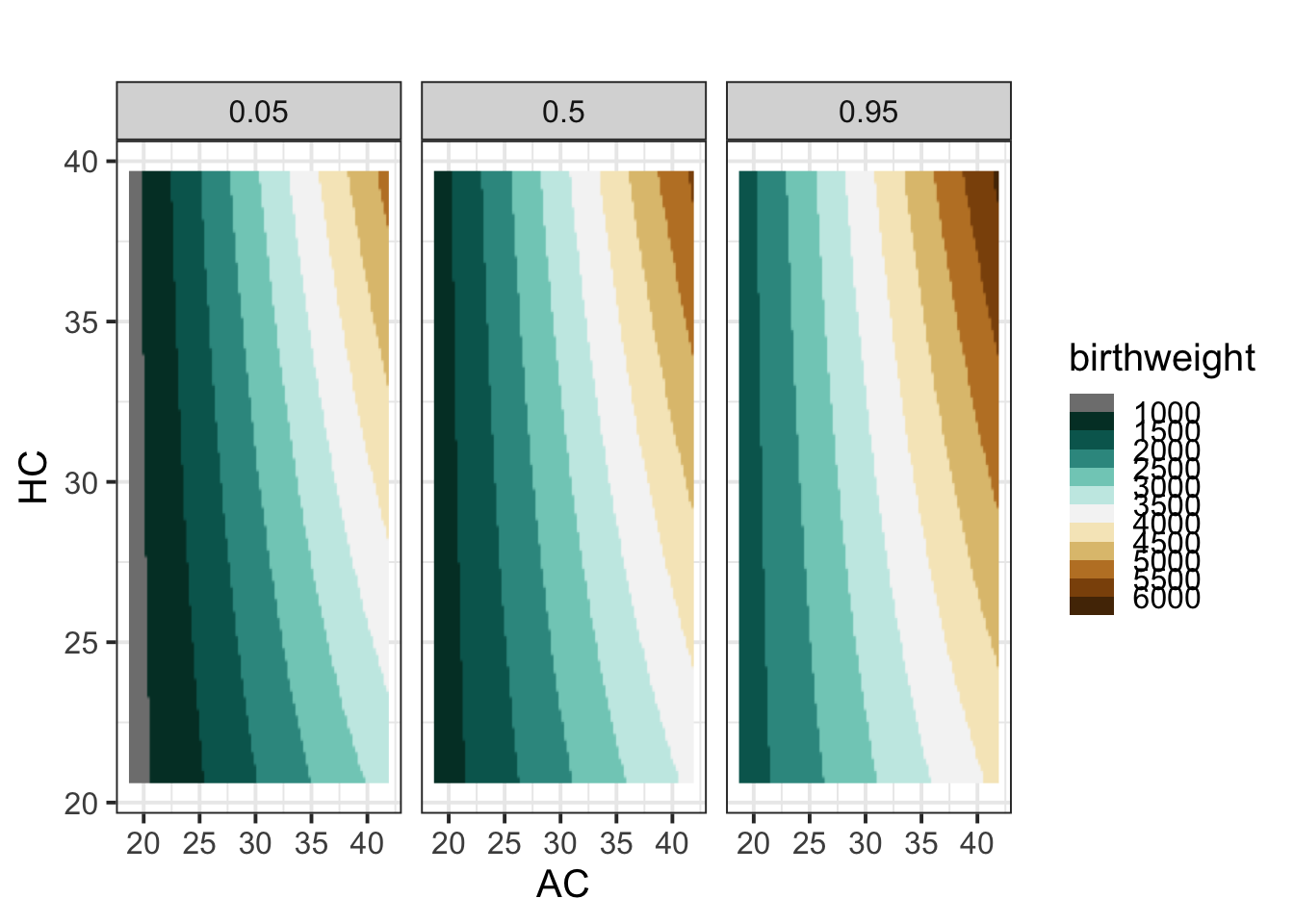
Figure 8.17
pe_pdf_grid(LM7.jsu.aic, terms=c("DBD", "AC", "HC", "parity", "FL"))