library(bamlss)
library(BayesX)
library(spdep)12: Socioeconomic Determinants of Federal Election Outcomes in Germany
Read the data
datensatz <- readRDS("data/datensatz_destatis.rds")
datensatz$nuts <- as.factor(as.character(datensatz$nuts))
m <- read.bnd("data/germany_nuts.bnd")Note: map consists of 64 polygons
Note: map consists of 38 regions
Reading map ... finished12.2 Estimation Results
Model Estimation
Compute neighborhood penalty matrix.
nb <- poly2nb(bnd2sp(m))
K <- nb2mat(nb, style = "B", zero.policy = TRUE)
K[K > 0] <- -1Number of neighbors
diag(K) <- apply(K, 1, function(x) { sum(abs(x)) })
colnames(K) <- rownames(K)Dirichlet model
f <- list(
Sonstige ~ s(nuts, bs = "mrf", xt = list(penalty = K))
+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung),
LINKE ~ s(nuts, bs = "mrf", xt = list(penalty = K)
)+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung),
FDP ~ s(nuts, bs = "mrf", xt = list(penalty = K)
)+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung),
GRUENE ~ s(nuts, bs = "mrf", xt = list(penalty = K)
)+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung),
SPD ~ s(nuts, bs = "mrf", xt = list(penalty = K)
)+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung),
CDUCSU ~ s(nuts, bs = "mrf", xt = list(penalty = K)
)+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung),
AfD ~ s(nuts, bs = "mrf", xt = list(penalty = K)
)+ s(AQ)+s(BIPpEW)+s(Wahlbeteiligung)
)b <- bamlss(f, data = datensatz, family = dirichlet_bamlss(k=7), optimizer = FALSE,
n.iter = 12000, burnin = 2000, thin = 10)summary(b)
Call:
bamlss(formula = f, family = dirichlet_bamlss(k = 7), data = datensatz,
optimizer = FALSE, n.iter = 12000, burnin = 2000, thin = 10)
---
Family: dirichlet
Link function: alpha1 = log, alpha2 = log, alpha3 = log, alpha4 = log, alpha5 = log, alpha6 = log, alpha7 = log
*---
Formula alpha1:
---
Sonstige ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) +
s(BIPpEW) + s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 3.099 3.037 3.100 3.16
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9977 0.9809 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 5.871e-03 3.132e-03 5.618e-03 0.010
s(nuts).alpha 8.351e-01 3.721e-01 9.122e-01 1.000
s(nuts).edf 2.888e+01 2.517e+01 2.905e+01 31.989
s(AQ).tau21 8.027e-01 9.327e-02 5.478e-01 2.802
s(AQ).alpha 9.568e-01 7.228e-01 9.936e-01 1.000
s(AQ).edf 5.151e+00 3.469e+00 5.098e+00 7.069
s(BIPpEW).tau21 1.232e-01 1.226e-04 1.520e-02 1.020
s(BIPpEW).alpha 9.621e-01 7.095e-01 9.979e-01 1.000
s(BIPpEW).edf 1.743e+00 1.003e+00 1.324e+00 3.886
s(Wahlbeteiligung).tau21 1.474e-01 7.592e-04 7.411e-02 0.790
s(Wahlbeteiligung).alpha 9.694e-01 7.537e-01 1.000e+00 1.000
s(Wahlbeteiligung).edf 3.620e+00 1.221e+00 3.589e+00 5.997
---
Formula alpha2:
---
LINKE ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) +
s(BIPpEW) + s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 3.558 3.497 3.559 3.614
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9977 0.9803 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 1.616e-02 8.897e-03 1.556e-02 0.027
s(nuts).alpha 8.453e-01 3.276e-01 9.298e-01 1.000
s(nuts).edf 3.476e+01 3.359e+01 3.482e+01 35.655
s(AQ).tau21 1.267e-01 1.061e-03 5.854e-02 0.688
s(AQ).alpha 9.813e-01 8.487e-01 1.000e+00 1.000
s(AQ).edf 3.403e+00 1.291e+00 3.309e+00 5.756
s(BIPpEW).tau21 8.124e-01 1.440e-04 1.450e-01 5.693
s(BIPpEW).alpha 9.478e-01 5.449e-01 9.989e-01 1.000
s(BIPpEW).edf 2.890e+00 1.008e+00 2.722e+00 6.240
s(Wahlbeteiligung).tau21 3.416e-02 1.015e-04 6.925e-03 0.194
s(Wahlbeteiligung).alpha 9.877e-01 8.948e-01 1.000e+00 1.000
s(Wahlbeteiligung).edf 2.400e+00 1.045e+00 2.089e+00 5.216
---
Formula alpha3:
---
FDP ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) + s(BIPpEW) +
s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 3.787 3.727 3.787 3.844
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9979 0.9790 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 6.166e-03 3.270e-03 5.862e-03 0.011
s(nuts).alpha 8.697e-01 4.239e-01 9.599e-01 1.000
s(nuts).edf 3.213e+01 2.961e+01 3.223e+01 34.216
s(AQ).tau21 2.235e-02 8.598e-05 2.723e-03 0.181
s(AQ).alpha 9.914e-01 9.458e-01 9.998e-01 1.000
s(AQ).edf 1.904e+00 1.026e+00 1.569e+00 4.452
s(BIPpEW).tau21 1.145e-01 1.614e-04 2.167e-02 0.817
s(BIPpEW).alpha 9.701e-01 7.320e-01 1.000e+00 1.000
s(BIPpEW).edf 1.978e+00 1.008e+00 1.694e+00 4.196
s(Wahlbeteiligung).tau21 2.493e-02 8.402e-05 4.281e-03 0.147
s(Wahlbeteiligung).alpha 9.863e-01 9.039e-01 9.991e-01 1.000
s(Wahlbeteiligung).edf 2.215e+00 1.032e+00 1.942e+00 4.878
---
Formula alpha4:
---
GRUENE ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) +
s(BIPpEW) + s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 3.495 3.435 3.496 3.554
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9977 0.9796 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 1.223e-02 7.024e-03 1.161e-02 0.020
s(nuts).alpha 8.379e-01 3.389e-01 9.374e-01 1.000
s(nuts).edf 3.363e+01 3.197e+01 3.365e+01 35.007
s(AQ).tau21 2.710e-01 7.695e-03 1.165e-01 1.424
s(AQ).alpha 9.684e-01 7.723e-01 1.000e+00 1.000
s(AQ).edf 3.967e+00 1.940e+00 3.829e+00 6.636
s(BIPpEW).tau21 1.732e+00 1.419e-01 9.502e-01 7.958
s(BIPpEW).alpha 9.159e-01 4.371e-01 9.971e-01 1.000
s(BIPpEW).edf 4.496e+00 2.773e+00 4.387e+00 6.913
s(Wahlbeteiligung).tau21 1.516e-02 9.452e-05 2.662e-03 0.099
s(Wahlbeteiligung).alpha 9.897e-01 9.311e-01 9.994e-01 1.000
s(Wahlbeteiligung).edf 1.890e+00 1.025e+00 1.574e+00 4.240
---
Formula alpha5:
---
SPD ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) + s(BIPpEW) +
s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 4.446 4.387 4.447 4.5
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9986 0.9859 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 1.164e-02 6.526e-03 1.106e-02 0.020
s(nuts).alpha 8.971e-01 5.204e-01 9.785e-01 1.000
s(nuts).edf 3.528e+01 3.431e+01 3.531e+01 36.050
s(AQ).tau21 1.737e-02 7.085e-05 2.592e-03 0.112
s(AQ).alpha 9.918e-01 9.452e-01 9.994e-01 1.000
s(AQ).edf 2.130e+00 1.045e+00 1.811e+00 4.868
s(BIPpEW).tau21 6.408e-01 4.569e-02 4.106e-01 2.660
s(BIPpEW).alpha 9.640e-01 7.356e-01 9.982e-01 1.000
s(BIPpEW).edf 4.209e+00 2.309e+00 4.180e+00 6.380
s(Wahlbeteiligung).tau21 1.856e-02 6.827e-05 2.372e-03 0.130
s(Wahlbeteiligung).alpha 9.910e-01 9.350e-01 9.999e-01 1.000
s(Wahlbeteiligung).edf 2.295e+00 1.048e+00 1.915e+00 5.301
---
Formula alpha6:
---
CDUCSU ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) +
s(BIPpEW) + s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 5.006 4.948 5.006 5.063
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9991 0.9928 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 2.624e-03 8.347e-04 2.443e-03 0.005
s(nuts).alpha 9.376e-01 6.821e-01 9.979e-01 1.000
s(nuts).edf 3.193e+01 2.721e+01 3.231e+01 34.494
s(AQ).tau21 1.506e-01 6.615e-03 9.212e-02 0.651
s(AQ).alpha 9.735e-01 8.269e-01 1.000e+00 1.000
s(AQ).edf 4.796e+00 2.528e+00 4.805e+00 6.921
s(BIPpEW).tau21 3.376e-01 2.023e-04 1.524e-01 1.873
s(BIPpEW).alpha 9.747e-01 8.234e-01 1.000e+00 1.000
s(BIPpEW).edf 3.486e+00 1.018e+00 3.652e+00 6.449
s(Wahlbeteiligung).tau21 1.529e-02 9.436e-05 3.599e-03 0.099
s(Wahlbeteiligung).alpha 9.925e-01 9.483e-01 1.000e+00 1.000
s(Wahlbeteiligung).edf 2.543e+00 1.092e+00 2.358e+00 5.318
---
Formula alpha7:
---
AfD ~ s(nuts, bs = "mrf", xt = list(penalty = K)) + s(AQ) + s(BIPpEW) +
s(Wahlbeteiligung)
-
Parametric coefficients:
Mean 2.5% 50% 97.5%
(Intercept) 4.015 3.955 4.016 4.073
-
Acceptance probability:
Mean 2.5% 50% 97.5%
alpha 0.9981 0.9842 1.0000 1
-
Smooth terms:
Mean 2.5% 50% 97.5%
s(nuts).tau21 0.009409 0.005172 0.008974 0.016
s(nuts).alpha 0.877560 0.445931 0.966131 1.000
s(nuts).edf 34.154575 32.567744 34.211444 35.321
s(AQ).tau21 0.452852 0.051485 0.309081 1.730
s(AQ).alpha 0.961224 0.774296 0.995965 1.000
s(AQ).edf 5.443384 3.523721 5.454842 7.436
s(BIPpEW).tau21 0.689729 0.047085 0.440677 2.664
s(BIPpEW).alpha 0.953893 0.664817 0.997266 1.000
s(BIPpEW).edf 3.959756 2.013702 3.884522 5.964
s(Wahlbeteiligung).tau21 0.154113 0.015258 0.095732 0.656
s(Wahlbeteiligung).alpha 0.976892 0.851216 1.000000 1.000
s(Wahlbeteiligung).edf 4.673583 2.980359 4.602879 6.832
---
Sampler summary:
-
DIC = -13477.42 logLik = 6879.439 pd = 281.4603
runtime = 3186.89
---MCMC Diagnostics
MCMC sampling path
samples <- data.frame(b$samples[[1]])
samples_FDP <- samples[,147:230]Plot as a MCMC sample examplatory the parameter path for the spatial covariate of FDP in Berlin
par(mar=c(5,5,4,2))
plot(samples_FDP$alpha3.s.s.nuts..x12,type="l", cex.main = 1,
main = expression("(a) MCMC sampling path of"~ beta["3,"~spat[12]]),
xlab = "Iterations", ylab = expression(beta["3,"~spat[12]]),
cex.lab = 1, cex.axis = 0.75)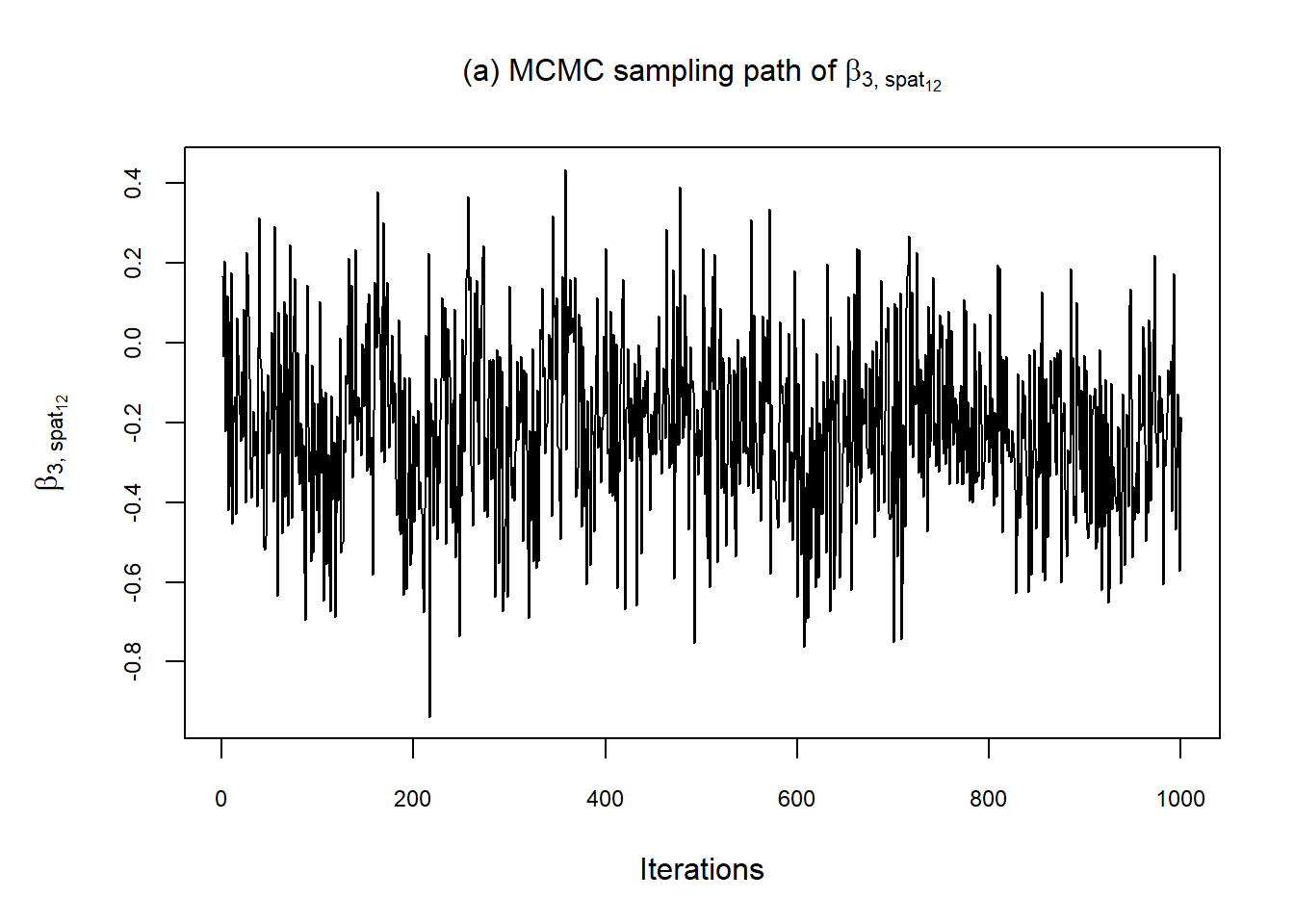
ACF plot and effective sample size
samples <- data.frame(samples_FDP$alpha3.s.s.nuts..x12)
samples <- as.mcmc(samples)
effectiveSize(samples)samples_FDP.alpha3.s.s.nuts..x12
217.5216 samples <- unname(samples)
autocorr.plot(samples, auto.layout = F, cex.main = 1, cex.axis = 0.75, cex.lab = 1,
main = expression("(b) ACF plot of"~beta["3,"~spat[12]]), lwd = 3)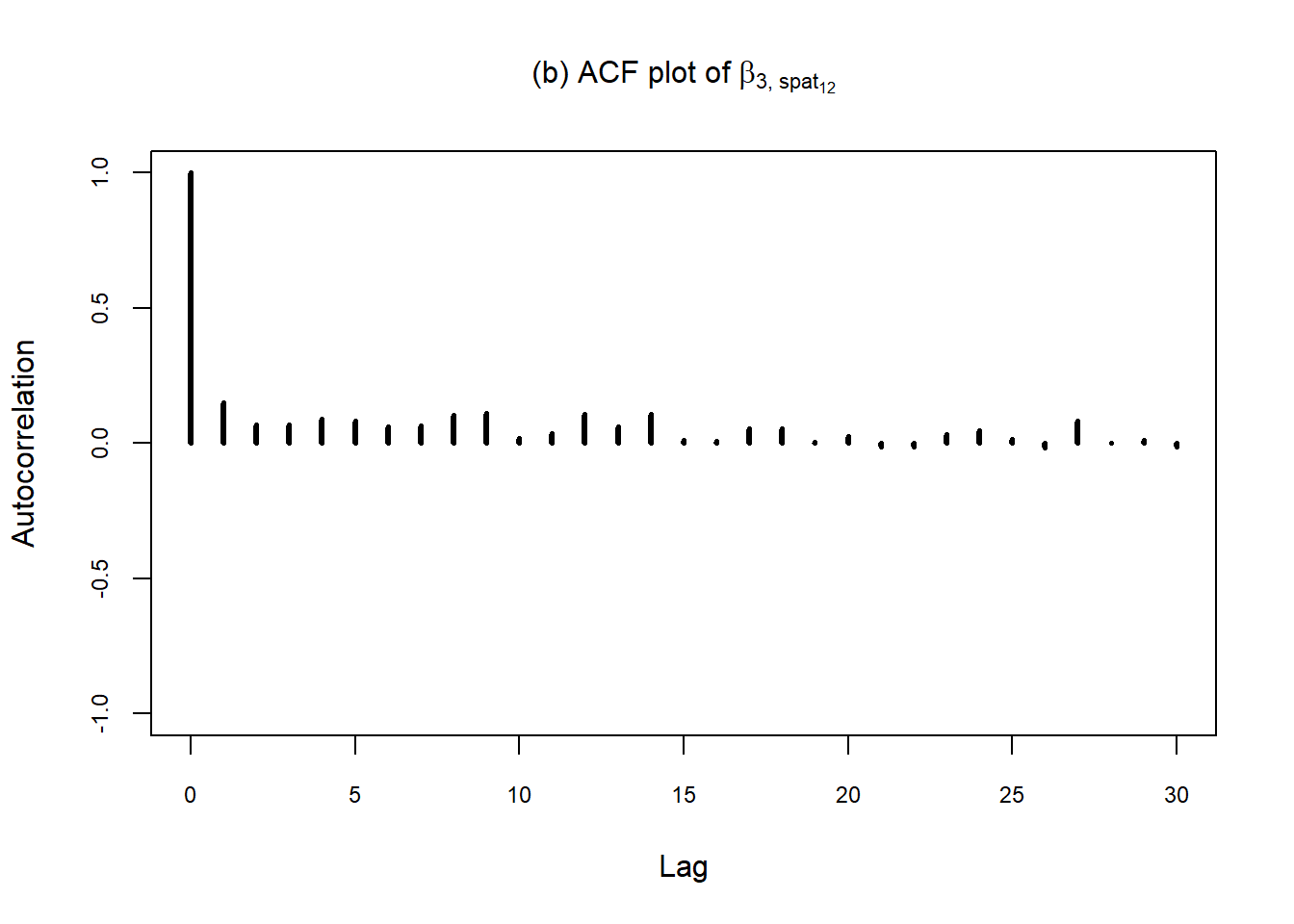
12.3 Scenario Analysis
Calculation of Predictions
Berlin: 11000; Munich: 9184
nd <- datensatz[datensatz$Kreisnummer %in% c(11000, 9184),
c("AQ", "BIPpEW", "Wahlbeteiligung", "nuts")]
nd <- rbind(datensatz[datensatz$Kreisnummer %in% c(11000, 9184),
c("AQ", "BIPpEW", "Wahlbeteiligung", "nuts")], nd)
nd[c(3, 4), "AQ"] <- 5.5
covariates <- nd[, -4]
covariates <- cbind(data.frame(City = rep(c("Munich", "Berlin"), 2)), covariates)
rownames(covariates) <- NULL
colnames(covariates) <- c("City", "UE", "GDPpC", "PoE")
cat("True and assumed covariates:\n")True and assumed covariates:covariates City UE GDPpC PoE
1 Munich 2.6 100475 83.9
2 Berlin 9.0 36798 75.6
3 Munich 5.5 100475 83.9
4 Berlin 5.5 36798 75.6pred <-
predict(
b,
newdata = nd,
what = "samples",
term = c("s(AQ)", "s(BIPpEW)", "s(Wahlbeteiligung)", "s(nuts)"),
FUN = function(x) {
x
},
intercept = TRUE
)
pred = lapply(
1:7,
FUN = function(x)
pred[[x]] <- matrix(unlist(pred[[x]]), nrow = 4)
)
names(pred) <- names(b[["y"]])
Nenner <-
((exp(pred$CDUCSU)) + (exp(pred$SPD)) + (exp(pred$GRUENE)) +
(exp(pred$FDP)) + (exp(pred$LINKE)) + (exp(pred$AfD)) + (exp(pred$Sonstige)))
csu <- exp(pred$CDUCSU)
afd <- exp(pred$AfD)
spd <- exp(pred$SPD)
fdp <- exp(pred$FDP)
linke <- exp(pred$LINKE)
gruene <- exp(pred$GRUENE)
sonstige <- exp(pred$Sonstige)
nd$CDUCSU_real <- rowMeans(exp(pred$CDUCSU) / Nenner)
nd$AfD_real <- rowMeans(exp(pred$AfD) / Nenner)
nd$SPD_real <- rowMeans(exp(pred$SPD) / Nenner)
nd$FDP_real <- rowMeans(exp(pred$FDP) / Nenner)
nd$LINKE_real <- rowMeans(exp(pred$LINKE) / Nenner)
nd$GRUENE_real <- rowMeans(exp(pred$GRUENE) / Nenner)
nd$Sonstige_real <- rowMeans(exp(pred$Sonstige) / Nenner)
vs_true <- datensatz[datensatz$Kreisnummer %in% c(11000, 9184), 6:12]
vs_true <- round(vs_true[, c(1, 2, 6, 3, 4, 5, 7)], 2)
vs_true <- cbind(data.frame(City = c("Munich", "Berlin")), vs_true)
rownames(vs_true) <- NULL
colnames(vs_true) <-
c("City", "CDU/CSU","SPD", "AfD", "The Greens","The Liberals","The Left","Others")
cat("Observed voting shares:\n")Observed voting shares:vs_true City CDU/CSU SPD AfD The Greens The Liberals The Left Others
1 Munich 0.37 0.14 0.09 0.13 0.15 0.05 0.06
2 Berlin 0.23 0.18 0.12 0.13 0.09 0.19 0.07vs_pred_mean <- round(nd[, c(1, 5, 7, 6, 10, 8, 9, 11)], 2)
vs_pred_mean <- cbind(data.frame(City = rep(c("Munich", "Berlin"), 2)), vs_pred_mean)
rownames(vs_pred_mean) <- NULL
colnames(vs_pred_mean) <-
c("City", "UE", "CDU/CSU","SPD", "AfD", "The Greens","The Liberals","The Left","Others")
cat("Predicted voting shares - mean:\n")Predicted voting shares - mean:vs_pred_mean City UE CDU/CSU SPD AfD The Greens The Liberals The Left Others
1 Munich 2.6 0.34 0.12 0.09 0.17 0.14 0.07 0.07
2 Berlin 9.0 0.23 0.18 0.13 0.12 0.09 0.19 0.07
3 Munich 5.5 0.25 0.14 0.07 0.24 0.14 0.10 0.06
4 Berlin 5.5 0.29 0.17 0.13 0.10 0.10 0.16 0.06nd <- datensatz[datensatz$Kreisnummer %in% c(11000, 9184),
c("AQ", "BIPpEW", "Wahlbeteiligung", "nuts")]
nd <- rbind(datensatz[datensatz$Kreisnummer %in% c(11000, 9184),
c("AQ", "BIPpEW", "Wahlbeteiligung", "nuts")], nd)
nd[c(3, 4), "AQ"] <- 5.5
nd$CDUCSU_real <- apply(
exp(pred$CDUCSU) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
nd$AfD_real <- apply(
exp(pred$AfD) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
nd$SPD_real <- apply(
exp(pred$SPD) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
nd$FDP_real <- apply(
exp(pred$FDP) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
nd$LINKE_real <- apply(
exp(pred$LINKE) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
nd$GRUENE_real <- apply(
exp(pred$GRUENE) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
nd$Sonstige_real <- apply(
exp(pred$Sonstige) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.025
)
vs_pred_ci_lower <- round(nd[, c(1, 5, 7, 6, 10, 8, 9, 11)], 2)
vs_pred_ci_lower <- cbind(data.frame(City = rep(c("Munich", "Berlin"), 2)), vs_pred_ci_lower)
rownames(vs_pred_ci_lower) <- NULL
colnames(vs_pred_ci_lower) <-
c("City", "UE", "CDU/CSU","SPD", "AfD", "The Greens","The Liberals","The Left","Others")
cat("Predicted voting shares - lower CI limit:\n")Predicted voting shares - lower CI limit:vs_pred_ci_lower City UE CDU/CSU SPD AfD The Greens The Liberals The Left Others
1 Munich 2.6 0.32 0.11 0.08 0.14 0.13 0.06 0.06
2 Berlin 9.0 0.19 0.14 0.10 0.09 0.06 0.15 0.05
3 Munich 5.5 0.23 0.12 0.06 0.21 0.12 0.08 0.05
4 Berlin 5.5 0.24 0.14 0.10 0.07 0.07 0.12 0.04nd <- datensatz[datensatz$Kreisnummer %in% c(11000, 9184),
c("AQ", "BIPpEW", "Wahlbeteiligung", "nuts")]
nd <- rbind(datensatz[datensatz$Kreisnummer %in% c(11000, 9184),
c("AQ", "BIPpEW", "Wahlbeteiligung", "nuts")], nd)
nd[c(3, 4), "AQ"] <- 5.5
nd$CDUCSU_real <- apply(
exp(pred$CDUCSU) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
nd$AfD_real <- apply(
exp(pred$AfD) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
nd$SPD_real <- apply(
exp(pred$SPD) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
nd$FDP_real <- apply(
exp(pred$FDP) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
nd$LINKE_real <- apply(
exp(pred$LINKE) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
nd$GRUENE_real <- apply(
exp(pred$GRUENE) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
nd$Sonstige_real <- apply(
exp(pred$Sonstige) / Nenner,
FUN = quantile,
MARGIN = 1,
probs = 0.975
)
vs_pred_ci_upper <- round(nd[, c(1, 5, 7, 6, 10, 8, 9, 11)], 2)
vs_pred_ci_upper <- cbind(data.frame(City = rep(c("Munich", "Berlin"), 2)), vs_pred_ci_upper)
rownames(vs_pred_ci_upper) <- NULL
colnames(vs_pred_ci_upper) <-
c("City", "UE", "CDU/CSU","SPD", "AfD", "The Greens","The Liberals","The Left","Others")
cat("Predicted voting shares - upper CI limit:\n")Predicted voting shares - upper CI limit:vs_pred_ci_upper City UE CDU/CSU SPD AfD The Greens The Liberals The Left Others
1 Munich 2.6 0.37 0.14 0.10 0.19 0.16 0.08 0.08
2 Berlin 9.0 0.27 0.22 0.16 0.16 0.12 0.23 0.10
3 Munich 5.5 0.28 0.16 0.09 0.27 0.16 0.12 0.07
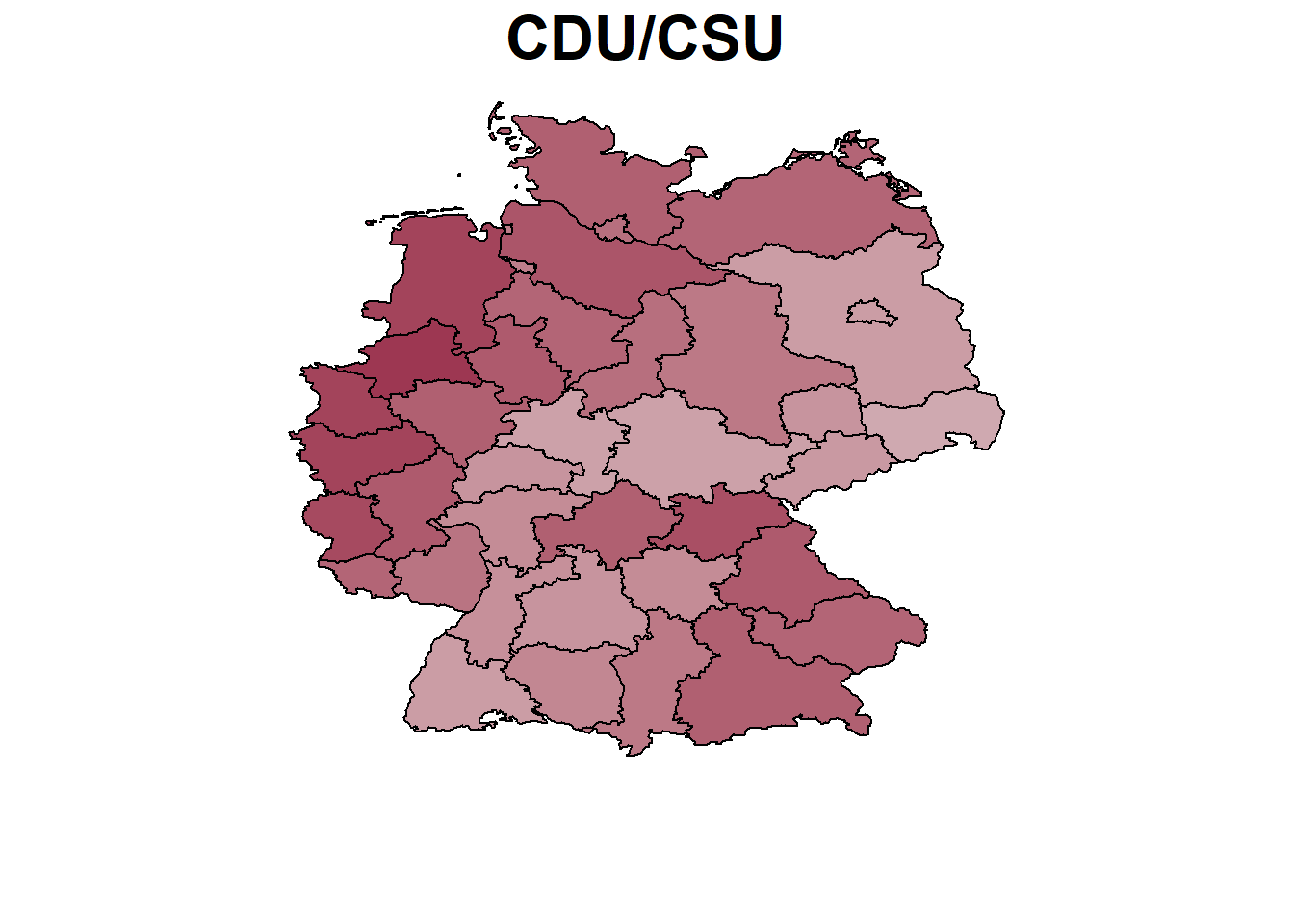
4 Berlin 5.5 0.34 0.21 0.16 0.13 0.13 0.20 0.09Plotting of Spatial Effects
parteien <- colnames(datensatz)[6:12]
nd <- unique(datensatz[, "nuts", drop = FALSE])
nd$AQ = mean(datensatz$AQ)
nd$BIPpEW = mean(datensatz$BIPpEW)
nd$Wahlbeteiligung = mean(datensatz$Wahlbeteiligung)
pred <-
predict(
b,
newdata = nd,
what = "samples",
term = c("s(AQ)", "s(BIPpEW)", "s(Wahlbeteiligung)", "s(nuts)"),
FUN = function(x) {x},
intercept = TRUE
)
names(pred) <- names(b[["y"]])
Nenner <-
rowMeans(
data.frame(exp(pred$CDUCSU)) + data.frame(exp(pred$SPD)) + data.frame(exp(pred$GRUENE)) +
data.frame(exp(pred$FDP)) + data.frame(exp(pred$LINKE)) + data.frame(exp(pred$AfD)) +
data.frame(exp(pred$Sonstige))
)
nd$CDUCSU_real <- rowMeans(exp(pred$CDUCSU)) / Nenner
nd$AfD_real <- rowMeans(exp(pred$AfD)) / Nenner
nd$SPD_real <- rowMeans(exp(pred$SPD)) / Nenner
nd$FDP_real <- rowMeans(exp(pred$FDP)) / Nenner
nd$LINKE_real <- rowMeans(exp(pred$LINKE)) / Nenner
nd$GRUENE_real <- rowMeans(exp(pred$GRUENE)) / Nenner
nd$Sonstige_real <- rowMeans(exp(pred$Sonstige)) / Nenner
# Translate parties
parties <- c("CDU/CSU","SPD","The Greens","The Liberals","The Left","AfD","Others")
par(mar=c(4,1,1.5,4))
for (x in parteien){
BayesX::drawmap(data = nd, map = m, regionvar = "nuts", plotvar = paste0(x,"_real"),
hcl.par=list(h = c(260, 0), c = 80, l = c(30, 90), power = 1.5),
legend = FALSE, limits = c(0,0.4), main = parties[which(parteien ==x)],
cex.main = 2)
}

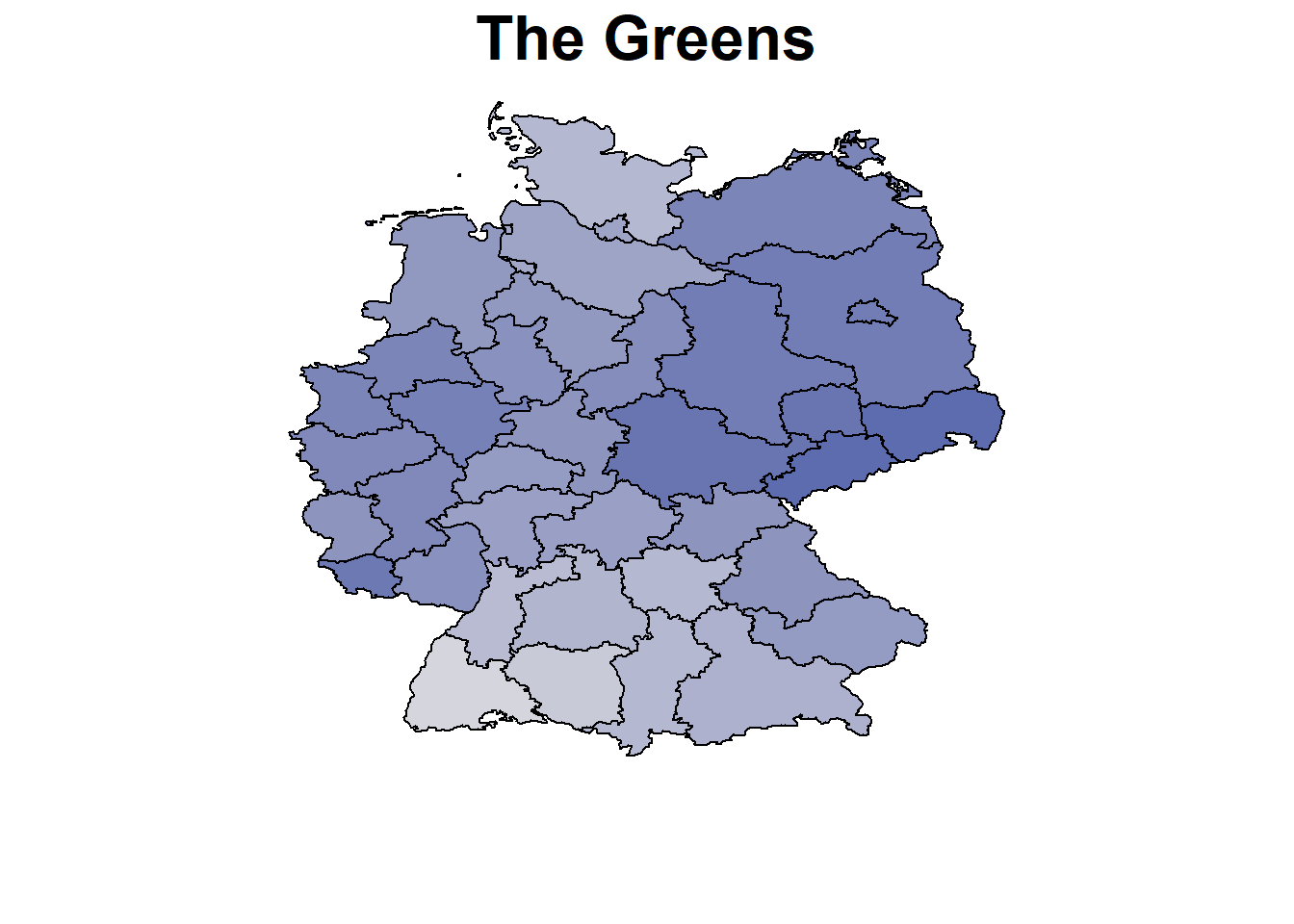
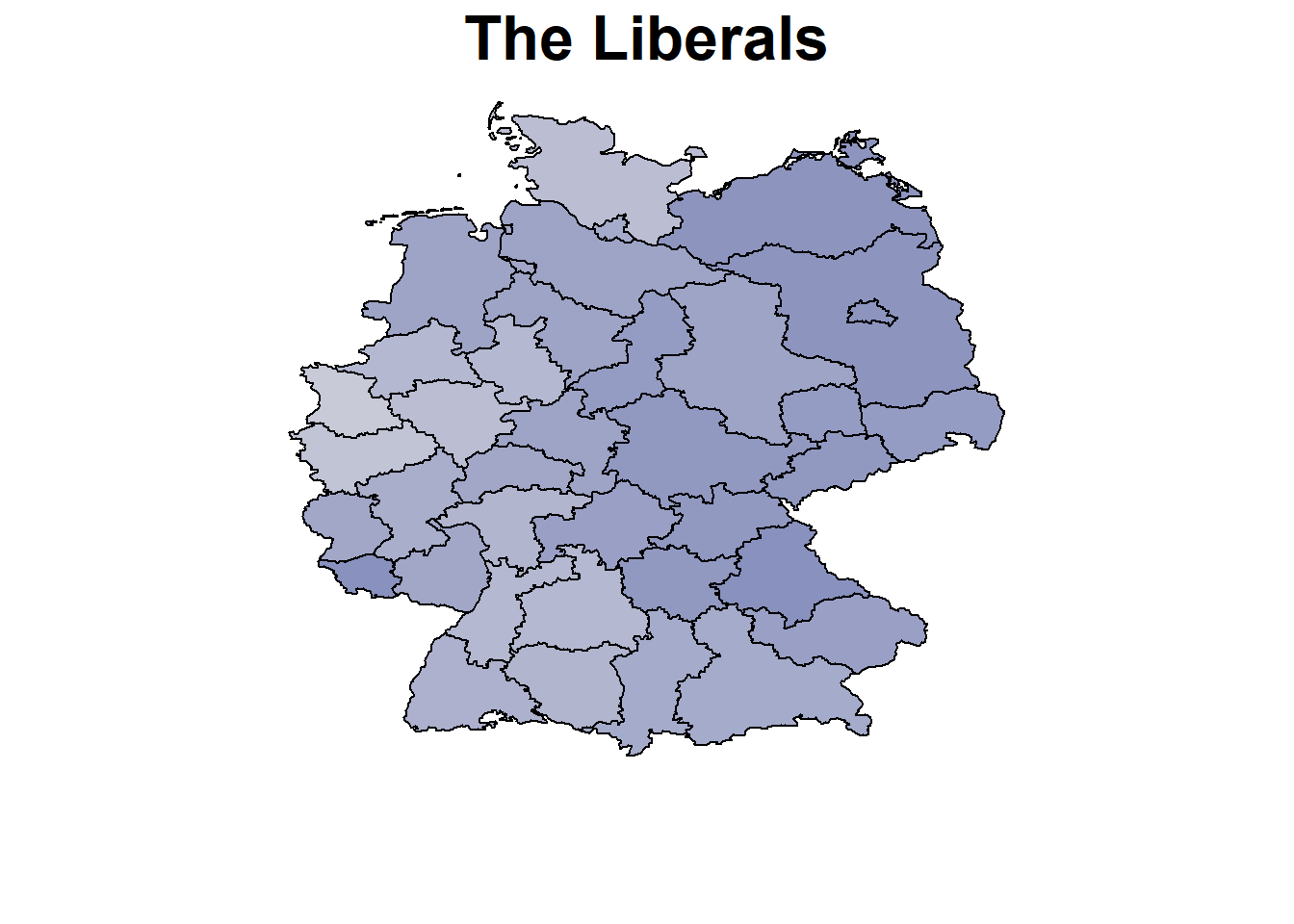
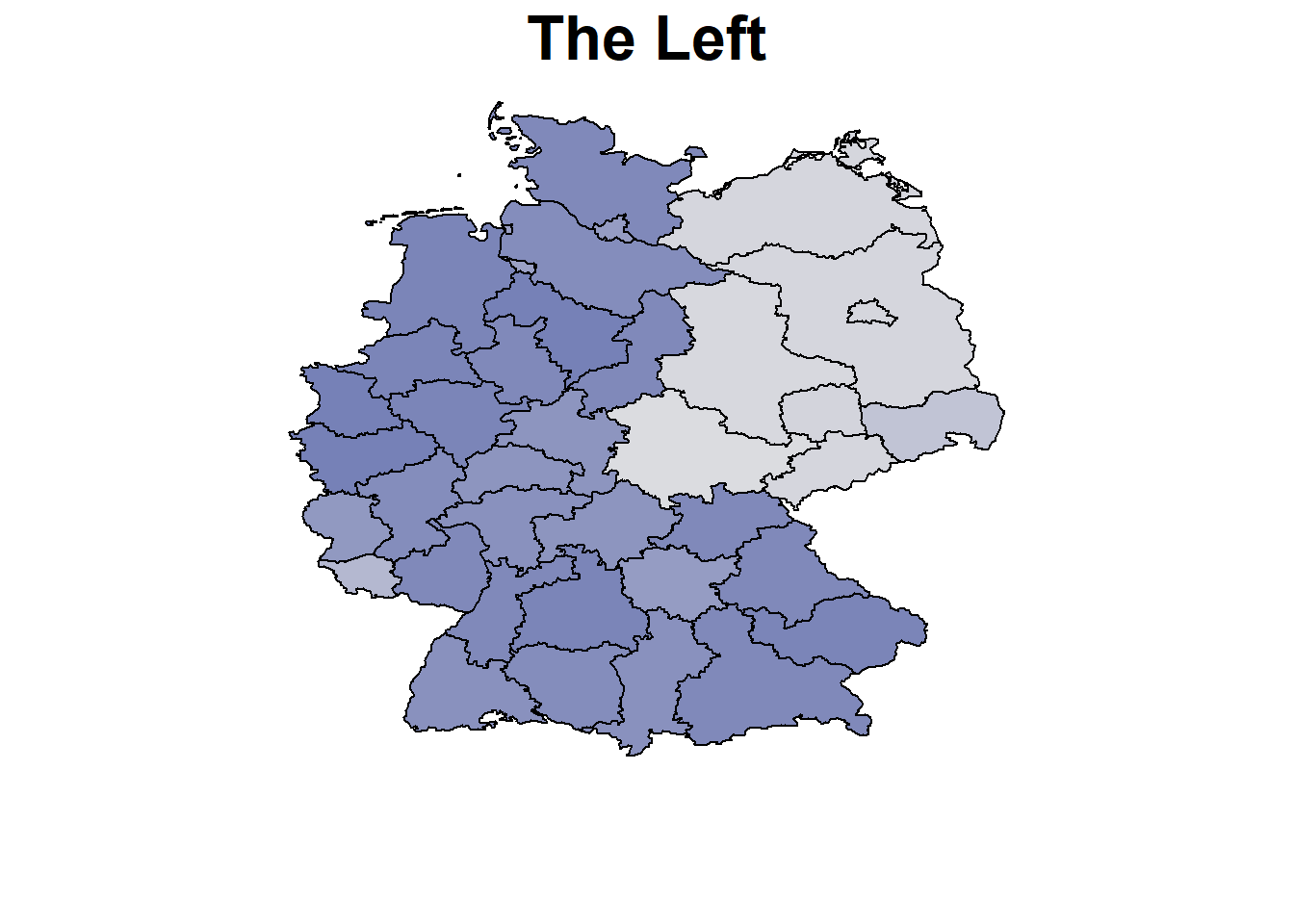
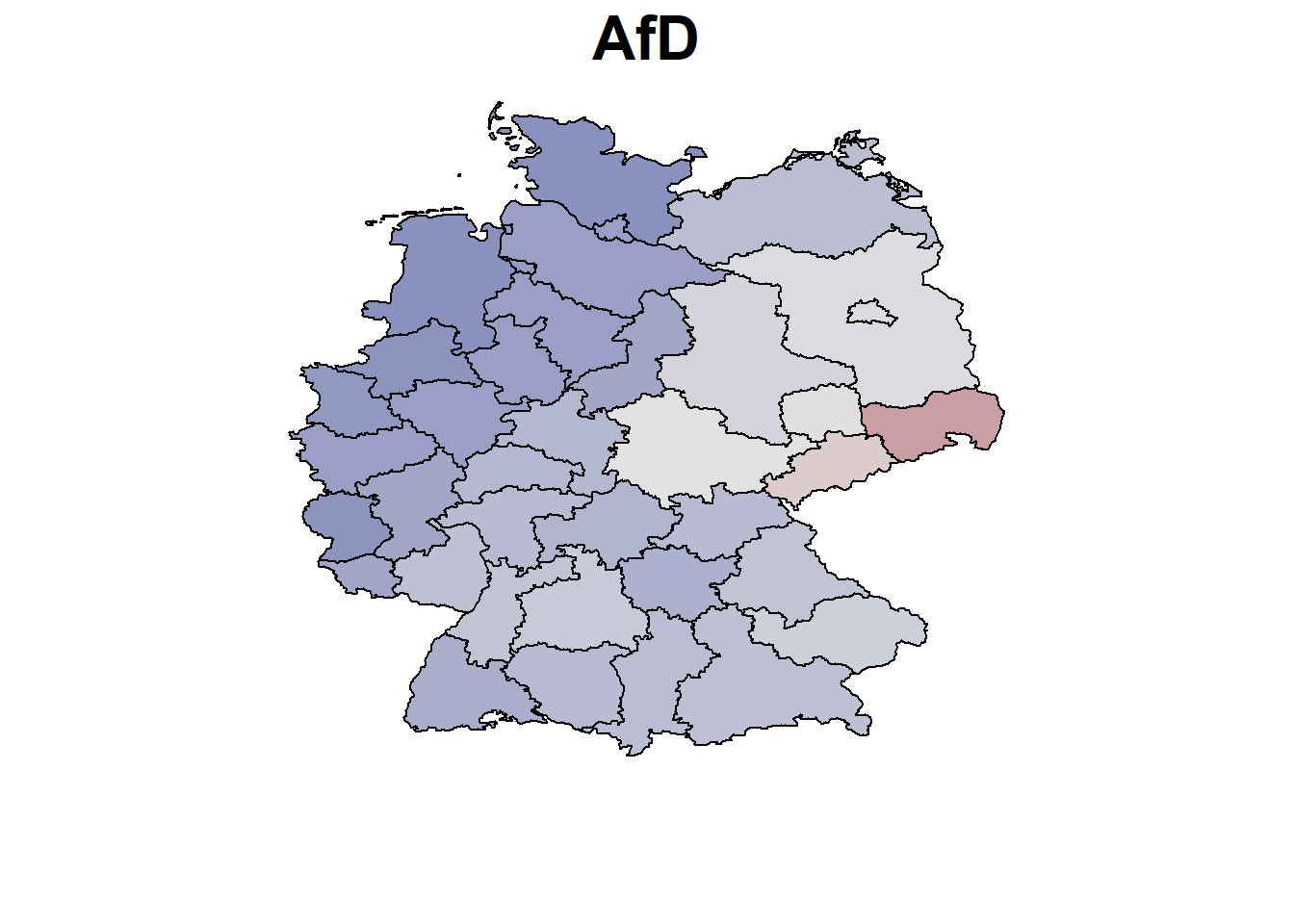
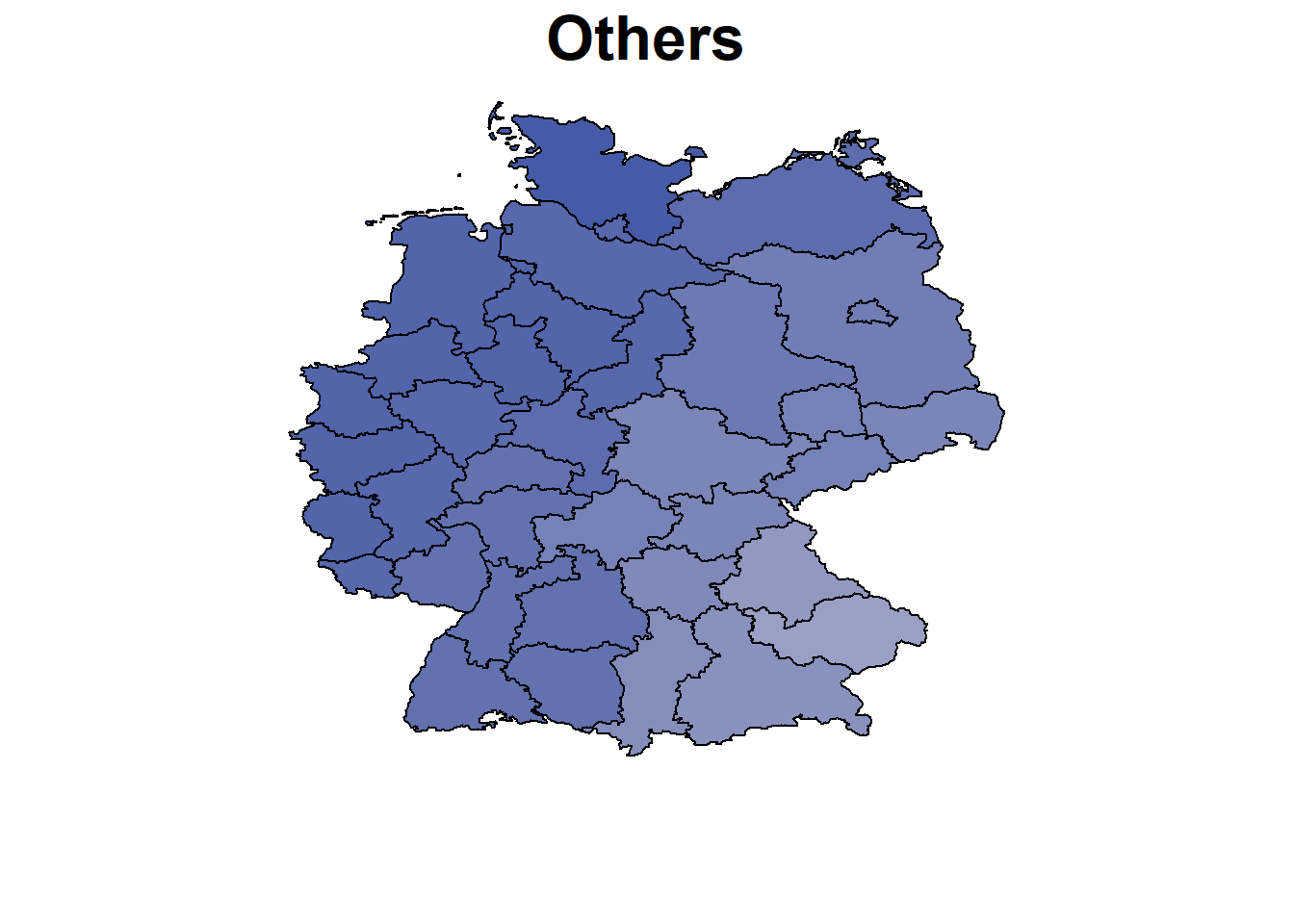
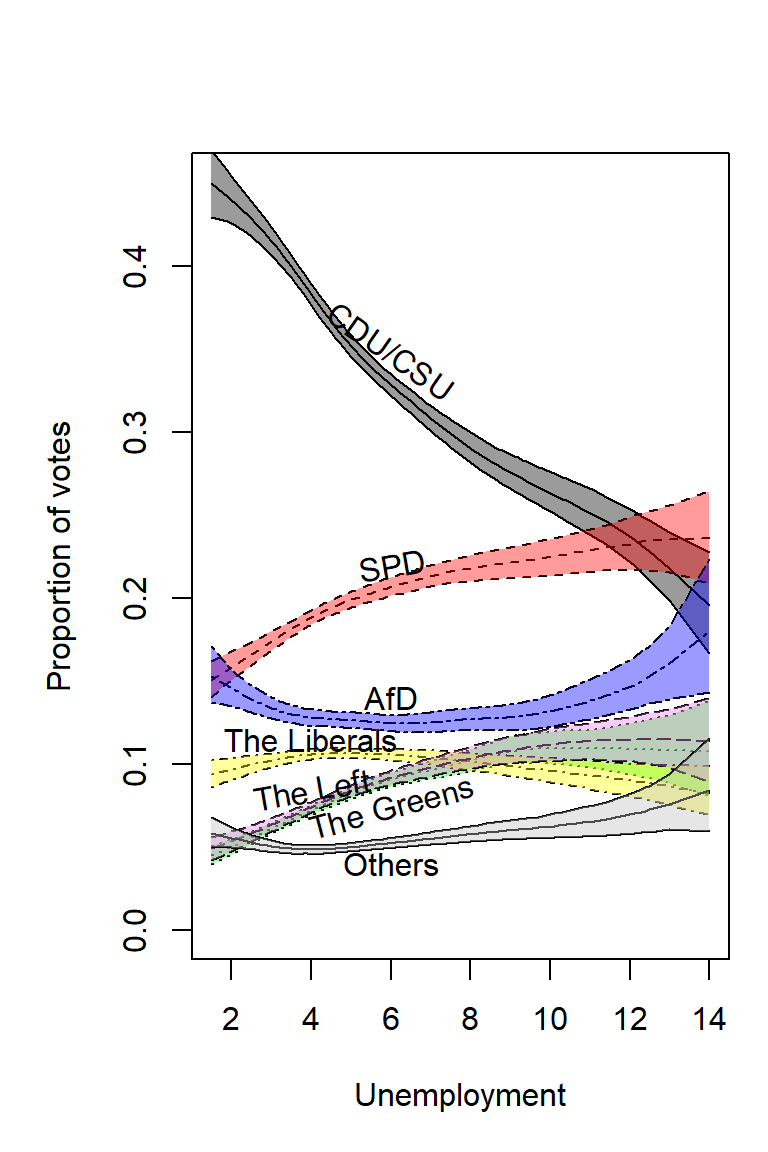
Calculation and Plotting of the Unemployment Effect
Set all covariates (without the one of interest) to their mean and do not include the spatial covariate nuts
data_aq <- unique(datensatz[, "AQ", drop = FALSE])
data_aq$BIPpEW <- mean(datensatz$BIPpEW)
data_aq$Wahlbeteiligung <- mean(datensatz$Wahlbeteiligung)
data_aq <- data_aq[order(data_aq$AQ), ]Predict the effect
pred_aq <-
predict(
b,
newdata = data_aq,
what = "samples",
term = c("s(AQ)", "s(BIPpEW)", "s(Wahlbeteiligung)"),
FUN = function(x) {
x
},
intercept = TRUE
)
names(pred_aq) <- names(b[["y"]])Save the enumerater according to the transformation formula
Nenner_aq <-
data.frame(exp(pred_aq$CDUCSU)) + data.frame(exp(pred_aq$SPD)) +
data.frame(exp(pred_aq$GRUENE)) + data.frame(exp(pred_aq$FDP)) +
data.frame(exp(pred_aq$LINKE)) + data.frame(exp(pred_aq$AfD)) +
data.frame(exp(pred_aq$Sonstige))
Nenner_aq_rm <-
rowMeans(
data.frame(exp(pred_aq$CDUCSU)) + data.frame(exp(pred_aq$SPD)) +
data.frame(exp(pred_aq$GRUENE)) + data.frame(exp(pred_aq$FDP)) +
data.frame(exp(pred_aq$LINKE)) + data.frame(exp(pred_aq$AfD)) +
data.frame(exp(pred_aq$Sonstige))
)Get the actual quantiles of the voting shares by transforming the estimated parameters rowwise
pred_aq_lq <- list()
pred_aq_lq$CDUCSU <-
apply(
exp(data.frame(pred_aq$CDUCSU)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_lq$SPD <-
apply(
exp(data.frame(pred_aq$SPD)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_lq$FDP <-
apply(
exp(data.frame(pred_aq$FDP)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_lq$LINKE <-
apply(
exp(data.frame(pred_aq$LINKE)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_lq$GRUENE <-
apply(
exp(data.frame(pred_aq$GRUENE)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_lq$AfD <-
apply(
exp(data.frame(pred_aq$AfD)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_lq$Sonstige <-
apply(
exp(data.frame(pred_aq$Sonstige)) / Nenner_aq,
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_aq_uq <- list()
pred_aq_uq$CDUCSU <-
apply(
exp(data.frame(pred_aq$CDUCSU)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_aq_uq$SPD <-
apply(
exp(data.frame(pred_aq$SPD)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_aq_uq$FDP <-
apply(
exp(data.frame(pred_aq$FDP)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_aq_uq$LINKE <-
apply(
exp(data.frame(pred_aq$LINKE)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_aq_uq$GRUENE <-
apply(
exp(data.frame(pred_aq$GRUENE)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_aq_uq$AfD <-
apply(
exp(data.frame(pred_aq$AfD)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_aq_uq$Sonstige <-
apply(
exp(data.frame(pred_aq$Sonstige)) / Nenner_aq,
FUN = "quantile",
prob = 0.975,
MAR = 1
)Get the means of the voting shares by transforming the estimated parameters rowwise
data_aq$CDUCSU_real <- rowMeans(exp(pred_aq$CDUCSU)) / Nenner_aq_rm
data_aq$AfD_real <- rowMeans(exp(pred_aq$AfD)) / Nenner_aq_rm
data_aq$SPD_real <- rowMeans(exp(pred_aq$SPD)) / Nenner_aq_rm
data_aq$FDP_real <- rowMeans(exp(pred_aq$FDP)) / Nenner_aq_rm
data_aq$LINKE_real <- rowMeans(exp(pred_aq$LINKE)) / Nenner_aq_rm
data_aq$GRUENE_real <- rowMeans(exp(pred_aq$GRUENE)) / Nenner_aq_rm
data_aq$Sonstige_real <- rowMeans(exp(pred_aq$Sonstige)) / Nenner_aq_rm
data_aq$CDUCSU_lq_real <- pred_aq_lq$CDUCSU
data_aq$AfD_lq_real <- pred_aq_lq$AfD
data_aq$SPD_lq_real <- pred_aq_lq$SPD
data_aq$FDP_lq_real <- pred_aq_lq$FDP
data_aq$LINKE_lq_real <- pred_aq_lq$LINKE
data_aq$GRUENE_lq_real <- pred_aq_lq$GRUENE
data_aq$Sonstige_lq_real <- pred_aq_lq$Sonstige
data_aq$CDUCSU_uq_real <- pred_aq_uq$CDUCSU
data_aq$AfD_uq_real <- pred_aq_uq$AfD
data_aq$SPD_uq_real <- pred_aq_uq$SPD
data_aq$FDP_uq_real <- pred_aq_uq$FDP
data_aq$LINKE_uq_real <- pred_aq_uq$LINKE
data_aq$GRUENE_uq_real <- pred_aq_uq$GRUENE
data_aq$Sonstige_uq_real <- pred_aq_uq$SonstigePlot the effects
cparties <- c("black","red","green","yellow","violet","blue","grey")
temp <- matrix(ncol=3,nrow=7)
for (j in 1:length(cparties)){
temp[j,]<-t(col2rgb(cparties[j]))
}
ptext<- c("CDU/CSU","SPD","The Greens","The Liberals","The Left","AfD","Others")
parteien<- c("CDUCSU", "SPD" ,"GRUENE" ,"FDP" , "LINKE","AfD","Sonstige")
angle = c(-35,10,15,0,10,0,0)
ytext = c(0.35,0.22,0.075,0.115,0.085,0.14,0.04)
xtext = c(6,6,6,4,4,6,6)
par(mar = c(5, 5, 4, 1))
j = 1
plot(
data_aq$AQ,
data_aq$CDUCSU_real,
type = "l",
col = "black",
xlab = "Unemployment",
ylab = "Proportion of votes",
ylim = c(0, 0.45),
cex.lab = 1,
cex.axis = 1
)
for (x in parteien){
lines(data_aq$AQ,data_aq[[paste(x,"_real",sep="")]] ,lty=j,lwd=1)
lines(data_aq$AQ,data_aq[[paste(x,"_uq_real",sep="")]] ,lty=j,lwd=1)
lines(data_aq$AQ,data_aq[[paste(x,"_lq_real",sep="")]] ,lty=j,lwd=1)
polygon(c(data_aq$AQ,rev(data_aq$AQ)),
c(data_aq[[paste(x,"_real",sep="")]],
rev(data_aq[[paste(x,"_lq_real",sep="")]])),
lty=2 ,border=NA,col=rgb(temp[j,1],temp[j,2],temp[j,3],alpha=100,
maxColorValue = 255))
polygon(c(data_aq$AQ,rev(data_aq$AQ)),
c(data_aq[[paste(x,"_real",sep="")]],
rev(data_aq[[paste(x,"_uq_real",sep="")]])) ,
border=NA,col=rgb(temp[j,1],temp[j,2],temp[j,3],alpha=100,
maxColorValue = 255))
text(x=xtext[j],y=ytext[j],paste(ptext[j]),srt = angle[j],cex = 1)
j=j+1
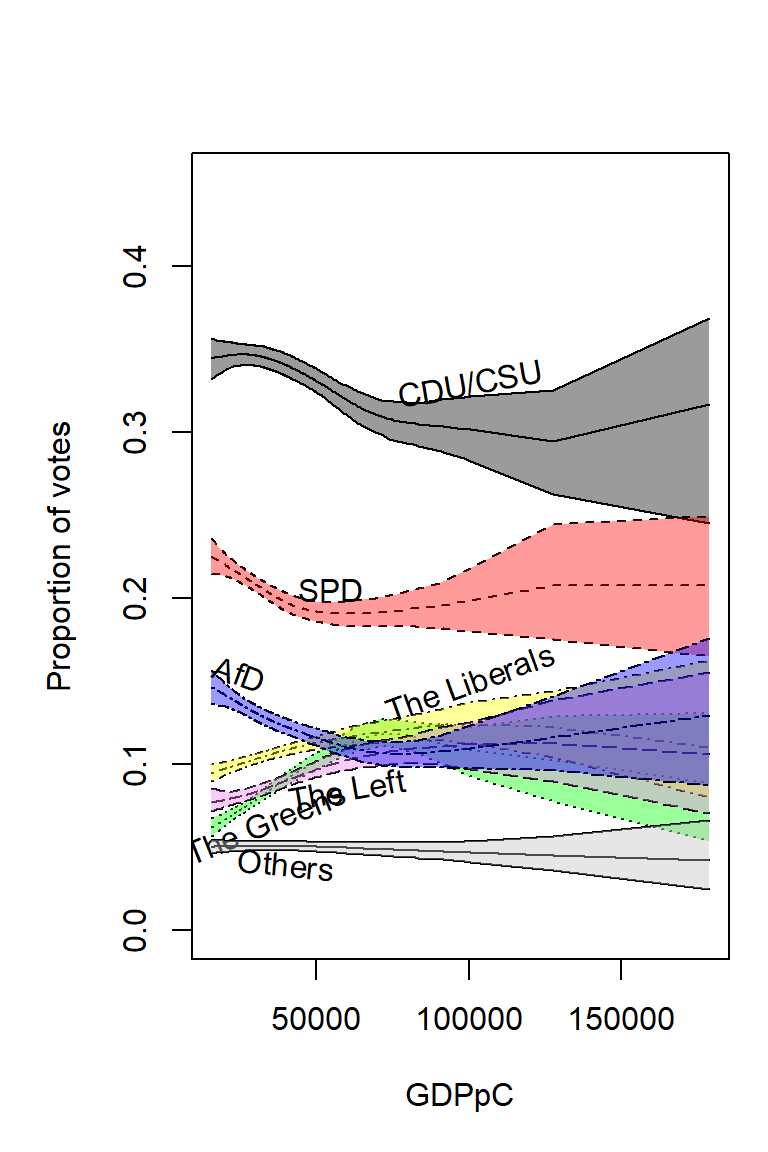
}
Calculation and Plotting of the GDPpC Effect
Set all covariates (without the one of interest) to their mean and do not include the spatial covariate nuts
data_BIPpEW <- unique(datensatz[, "BIPpEW", drop = FALSE])
data_BIPpEW$AQ <- mean(datensatz$AQ)
data_BIPpEW$Wahlbeteiligung <- mean(datensatz$Wahlbeteiligung)
data_BIPpEW <- data_BIPpEW[order(data_BIPpEW$BIPpEW), ]Predict the effect
pred_BIPpEW <-
predict(
b,
newdata = data_BIPpEW,
what = "samples",
term = c("s(AQ)", "s(BIPpEW)", "s(Wahlbeteiligung)"),
FUN = function(x) {
x
},
intercept = TRUE
)
names(pred_BIPpEW) <- names(b[["y"]])
Nenner_BIPpEW <-
data.frame(exp(pred_BIPpEW$CDUCSU)) + data.frame(exp(pred_BIPpEW$SPD)) +
data.frame(exp(pred_BIPpEW$GRUENE)) + data.frame(exp(pred_BIPpEW$FDP)) +
data.frame(exp(pred_BIPpEW$LINKE)) + data.frame(exp(pred_BIPpEW$AfD)) +
data.frame(exp(pred_BIPpEW$Sonstige))
Nenner_BIPpEW_rm <-
rowMeans(
data.frame(exp(pred_BIPpEW$CDUCSU)) + data.frame(exp(pred_BIPpEW$SPD)) +
data.frame(exp(pred_BIPpEW$GRUENE)) +
data.frame(exp(pred_BIPpEW$FDP)) + data.frame(exp(pred_BIPpEW$LINKE)) +
data.frame(exp(pred_BIPpEW$AfD)) + data.frame(exp(pred_BIPpEW$Sonstige))
)Get the actual quantiles of the voting shares by transforming the estimated parameters rowwise
pred_BIPpEW_lq <- list()
pred_BIPpEW_lq$CDUCSU <-
apply((exp(data.frame(pred_BIPpEW$CDUCSU)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_lq$SPD <-
apply((exp(data.frame(pred_BIPpEW$SPD)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_lq$FDP <-
apply((exp(data.frame(pred_BIPpEW$FDP)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_lq$LINKE <-
apply((exp(data.frame(pred_BIPpEW$LINKE)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_lq$GRUENE <-
apply((exp(data.frame(pred_BIPpEW$GRUENE)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_lq$AfD <-
apply((exp(data.frame(pred_BIPpEW$AfD)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_lq$Sonstige <-
apply((exp(data.frame(
pred_BIPpEW$Sonstige
)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.025,
MAR = 1)
pred_BIPpEW_uq <- list()
pred_BIPpEW_uq$CDUCSU <-
apply((exp(data.frame(pred_BIPpEW$CDUCSU)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)
pred_BIPpEW_uq$SPD <-
apply((exp(data.frame(pred_BIPpEW$SPD)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)
pred_BIPpEW_uq$FDP <-
apply((exp(data.frame(pred_BIPpEW$FDP)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)
pred_BIPpEW_uq$LINKE <-
apply((exp(data.frame(pred_BIPpEW$LINKE)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)
pred_BIPpEW_uq$GRUENE <-
apply((exp(data.frame(pred_BIPpEW$GRUENE)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)
pred_BIPpEW_uq$AfD <-
apply((exp(data.frame(pred_BIPpEW$AfD)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)
pred_BIPpEW_uq$Sonstige <-
apply((exp(data.frame(
pred_BIPpEW$Sonstige
)) / Nenner_BIPpEW),
FUN = "quantile",
prob = 0.975,
MAR = 1)Get the means of the voting shares by transforming the estimated parameters rowwise
data_BIPpEW$CDUCSU_real <-
rowMeans(exp(pred_BIPpEW$CDUCSU)) / Nenner_BIPpEW_rm
data_BIPpEW$AfD_real <-
rowMeans(exp(pred_BIPpEW$AfD)) / Nenner_BIPpEW_rm
data_BIPpEW$SPD_real <-
rowMeans(exp(pred_BIPpEW$SPD)) / Nenner_BIPpEW_rm
data_BIPpEW$FDP_real <-
rowMeans(exp(pred_BIPpEW$FDP)) / Nenner_BIPpEW_rm
data_BIPpEW$LINKE_real <-
rowMeans(exp(pred_BIPpEW$LINKE)) / Nenner_BIPpEW_rm
data_BIPpEW$GRUENE_real <-
rowMeans(exp(pred_BIPpEW$GRUENE)) / Nenner_BIPpEW_rm
data_BIPpEW$Sonstige_real <-
rowMeans(exp(pred_BIPpEW$Sonstige)) / Nenner_BIPpEW_rm
data_BIPpEW$CDUCSU_lq_real <- pred_BIPpEW_lq$CDUCSU
data_BIPpEW$AfD_lq_real <- pred_BIPpEW_lq$AfD
data_BIPpEW$SPD_lq_real <- pred_BIPpEW_lq$SPD
data_BIPpEW$FDP_lq_real <- pred_BIPpEW_lq$FDP
data_BIPpEW$LINKE_lq_real <- pred_BIPpEW_lq$LINKE
data_BIPpEW$GRUENE_lq_real <- pred_BIPpEW_lq$GRUENE
data_BIPpEW$Sonstige_lq_real <- pred_BIPpEW_lq$Sonstige
data_BIPpEW$CDUCSU_uq_real <- pred_BIPpEW_uq$CDUCSU
data_BIPpEW$AfD_uq_real <- pred_BIPpEW_uq$AfD
data_BIPpEW$SPD_uq_real <- pred_BIPpEW_uq$SPD
data_BIPpEW$FDP_uq_real <- pred_BIPpEW_uq$FDP
data_BIPpEW$LINKE_uq_real <- pred_BIPpEW_uq$LINKE
data_BIPpEW$GRUENE_uq_real <- pred_BIPpEW_uq$GRUENE
data_BIPpEW$Sonstige_uq_real <- pred_BIPpEW_uq$SonstigePlot the effects
cparties<-c("black","red","green","yellow","violet","blue","grey")
temp<-matrix(ncol=3,nrow=7)
for (j in 1:length(cparties)){
temp[j,]<-t(col2rgb(cparties[j]))
}
ptext<- c("CDU/CSU","SPD","The Greens","The Liberals","The Left","AfD","Others")
parteien<- c("CDUCSU", "SPD" , "GRUENE" , "FDP" ,"LINKE","AfD","Sonstige")
angle=c(10,0,22,20,10,-20,-5)
ytext=c(0.33,0.205,0.065,0.15,0.085,0.155,0.04)
xtext=c(100000,55000,33000,100000,60000,25000,40000)
par(mar=c(5,5,4,1))
j=1
plot(data_BIPpEW$BIPpEW,data_BIPpEW$CDUCSU_real,type = "l",
col="black",xlab="GDPpC",ylab="Proportion of votes",ylim=c(0,0.45),
cex.lab = 1,cex.axis=1)
for (x in parteien){
lines(data_BIPpEW$BIPpEW,data_BIPpEW[[paste(x,"_real",sep="")]] ,lty=j,lwd=1)
lines(data_BIPpEW$BIPpEW,data_BIPpEW[[paste(x,"_uq_real",sep="")]] ,lty=j,lwd=1)
lines(data_BIPpEW$BIPpEW,data_BIPpEW[[paste(x,"_lq_real",sep="")]] ,lty=j,lwd=1)
polygon(c(data_BIPpEW$BIPpEW,rev(data_BIPpEW$BIPpEW)),
c(data_BIPpEW[[paste(x,"_real",sep="")]],
rev(data_BIPpEW[[paste(x,"_lq_real",sep="")]])),lty=2,border=NA,
col=rgb(temp[j,1],temp[j,2],temp[j,3],alpha=100,maxColorValue = 255))
polygon(c(data_BIPpEW$BIPpEW,rev(data_BIPpEW$BIPpEW)),
c(data_BIPpEW[[paste(x,"_real",sep="")]],
rev(data_BIPpEW[[paste(x,"_uq_real",sep="")]])),
border=NA,col=rgb(temp[j,1],temp[j,2],temp[j,3],alpha=100,
maxColorValue = 255))
text(x=xtext[j],y=ytext[j],paste(ptext[j]),srt = angle[j],cex = 1)
j=j+1
}
Calculation and Plotting of the Turnout Effect
Set all covariates (without the one of interest) to their mean and do not include the spatial covariate nuts
data_Wahlbeteiligung <- unique(datensatz[, "Wahlbeteiligung", drop = FALSE])
data_Wahlbeteiligung$AQ <- mean(datensatz$AQ)
data_Wahlbeteiligung$BIPpEW <- mean(datensatz$BIPpEW)
data_Wahlbeteiligung <- data_Wahlbeteiligung[order(data_Wahlbeteiligung$Wahlbeteiligung), ]Predict the effect
pred_Wahlbeteiligung <-
predict(
b,
newdata = data_Wahlbeteiligung,
what = "samples",
term = c("s(AQ)", "s(BIPpEW)", "s(Wahlbeteiligung)"),
FUN = function(x) {
x
},
intercept = TRUE
)
names(pred_Wahlbeteiligung) <- names(b[["y"]])Save the enumerator according to the transformation formula
Nenner_Wahlbeteiligung <-
data.frame(exp(pred_Wahlbeteiligung$CDUCSU)) + data.frame(exp(pred_Wahlbeteiligung$SPD)) +
data.frame(exp(pred_Wahlbeteiligung$GRUENE)) + data.frame(exp(pred_Wahlbeteiligung$FDP)) +
data.frame(exp(pred_Wahlbeteiligung$LINKE)) + data.frame(exp(pred_Wahlbeteiligung$AfD)) +
data.frame(exp(pred_Wahlbeteiligung$Sonstige))
Nenner_Wahlbeteiligung_rm <-
rowMeans(
data.frame(exp(pred_Wahlbeteiligung$CDUCSU)) + data.frame(exp(pred_Wahlbeteiligung$SPD)) +
data.frame(exp(pred_Wahlbeteiligung$GRUENE)) +
data.frame(exp(pred_Wahlbeteiligung$FDP)) + data.frame(exp(pred_Wahlbeteiligung$LINKE)) +
data.frame(exp(pred_Wahlbeteiligung$AfD)) + data.frame(exp(pred_Wahlbeteiligung$Sonstige))
)Get the actual quantiles of the voting shares by transforming the estimated parameters rowwise
pred_Wahlbeteiligung_lq <- list()
pred_Wahlbeteiligung_lq$CDUCSU <-
apply((exp(
data.frame(pred_Wahlbeteiligung$CDUCSU)
) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_lq$SPD <-
apply((exp(data.frame(
pred_Wahlbeteiligung$SPD
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_lq$FDP <-
apply((exp(data.frame(
pred_Wahlbeteiligung$FDP
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_lq$LINKE <-
apply((exp(data.frame(
pred_Wahlbeteiligung$LINKE
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_lq$GRUENE <-
apply((exp(
data.frame(pred_Wahlbeteiligung$GRUENE)
) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_lq$AfD <-
apply((exp(data.frame(
pred_Wahlbeteiligung$AfD
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_lq$Sonstige <-
apply((exp(
data.frame(pred_Wahlbeteiligung$Sonstige)
) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.025,
MAR = 1
)
pred_Wahlbeteiligung_uq <- list()
pred_Wahlbeteiligung_uq$CDUCSU <-
apply((exp(
data.frame(pred_Wahlbeteiligung$CDUCSU)
) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_Wahlbeteiligung_uq$SPD <-
apply((exp(data.frame(
pred_Wahlbeteiligung$SPD
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_Wahlbeteiligung_uq$FDP <-
apply((exp(data.frame(
pred_Wahlbeteiligung$FDP
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_Wahlbeteiligung_uq$LINKE <-
apply((exp(data.frame(
pred_Wahlbeteiligung$LINKE
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_Wahlbeteiligung_uq$GRUENE <-
apply((exp(
data.frame(pred_Wahlbeteiligung$GRUENE)
) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_Wahlbeteiligung_uq$AfD <-
apply((exp(data.frame(
pred_Wahlbeteiligung$AfD
)) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)
pred_Wahlbeteiligung_uq$Sonstige <-
apply((exp(
data.frame(pred_Wahlbeteiligung$Sonstige)
) / Nenner_Wahlbeteiligung),
FUN = "quantile",
prob = 0.975,
MAR = 1
)Get the means of the voting shares by transforming the estimated parameters rowwise
data_Wahlbeteiligung$CDUCSU_real <-
rowMeans(exp(pred_Wahlbeteiligung$CDUCSU)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$AfD_real <-
rowMeans(exp(pred_Wahlbeteiligung$AfD)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$SPD_real <-
rowMeans(exp(pred_Wahlbeteiligung$SPD)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$FDP_real <-
rowMeans(exp(pred_Wahlbeteiligung$FDP)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$LINKE_real <-
rowMeans(exp(pred_Wahlbeteiligung$LINKE)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$GRUENE_real <-
rowMeans(exp(pred_Wahlbeteiligung$GRUENE)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$Sonstige_real <-
rowMeans(exp(pred_Wahlbeteiligung$Sonstige)) / Nenner_Wahlbeteiligung_rm
data_Wahlbeteiligung$CDUCSU_lq_real<-pred_Wahlbeteiligung_lq$CDUCSU
data_Wahlbeteiligung$AfD_lq_real<- pred_Wahlbeteiligung_lq$AfD
data_Wahlbeteiligung$SPD_lq_real<- pred_Wahlbeteiligung_lq$SPD
data_Wahlbeteiligung$FDP_lq_real<- pred_Wahlbeteiligung_lq$FDP
data_Wahlbeteiligung$LINKE_lq_real<- pred_Wahlbeteiligung_lq$LINKE
data_Wahlbeteiligung$GRUENE_lq_real<- pred_Wahlbeteiligung_lq$GRUENE
data_Wahlbeteiligung$Sonstige_lq_real<- pred_Wahlbeteiligung_lq$Sonstige
data_Wahlbeteiligung$CDUCSU_uq_real<- pred_Wahlbeteiligung_uq$CDUCSU
data_Wahlbeteiligung$AfD_uq_real<- pred_Wahlbeteiligung_uq$AfD
data_Wahlbeteiligung$SPD_uq_real<- pred_Wahlbeteiligung_uq$SPD
data_Wahlbeteiligung$FDP_uq_real<- pred_Wahlbeteiligung_uq$FDP
data_Wahlbeteiligung$LINKE_uq_real<- pred_Wahlbeteiligung_uq$LINKE
data_Wahlbeteiligung$GRUENE_uq_real<- pred_Wahlbeteiligung_uq$GRUENE
data_Wahlbeteiligung$Sonstige_uq_real<- pred_Wahlbeteiligung_uq$SonstigePlot the effects
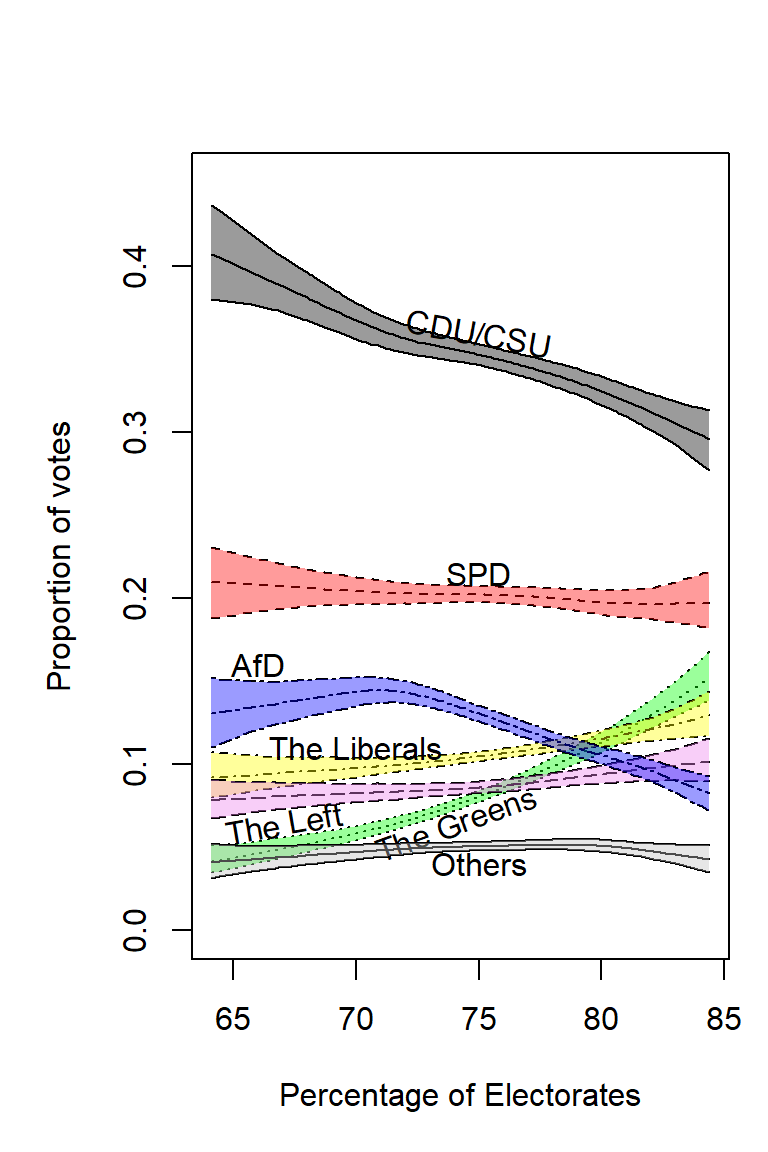
cparties<-c("black","red","green","yellow","violet","blue","grey")
temp<-matrix(ncol=3,nrow=7)
for (j in 1:length(cparties)){
temp[j,]<-t(col2rgb(cparties[j]))
}
ptext<- c("CDU/CSU","SPD","The Greens","The Liberals","The Left","AfD","Others")
parteien<- c("CDUCSU", "SPD", "GRUENE" , "FDP" , "LINKE", "AfD", "Sonstige")
angle=c(-10,0,20,0,10,0,0)
ytext=c(0.36,0.215,0.065,0.11,0.065,0.16,0.04)
xtext=c(75,75,74,70,67,66,75)
par(mar=c(5,5,4,1))
j=1
plot(data_Wahlbeteiligung$Wahlbeteiligung,data_Wahlbeteiligung$CDUCSU_real,type = "l",
col="black",xlab="Percentage of Electorates",
ylab="Proportion of votes",ylim=c(0,0.45), cex.lab = 1,cex.axis=1)
for (x in parteien){
lines(data_Wahlbeteiligung$Wahlbeteiligung,
data_Wahlbeteiligung[[paste(x,"_real",sep="")]] ,lty=j,lwd=1)
lines(data_Wahlbeteiligung$Wahlbeteiligung,
data_Wahlbeteiligung[[paste(x,"_uq_real",sep="")]] ,lty=j,lwd=1)
lines(data_Wahlbeteiligung$Wahlbeteiligung,
data_Wahlbeteiligung[[paste(x,"_lq_real",sep="")]] ,lty=j,lwd=1)
polygon(c(data_Wahlbeteiligung$Wahlbeteiligung,
rev(data_Wahlbeteiligung$Wahlbeteiligung)),
c(data_Wahlbeteiligung[[paste(x,"_real",sep="")]],
rev(data_Wahlbeteiligung[[paste(x,"_lq_real",sep="")]])),
lty=2 ,border=NA,col=rgb(temp[j,1],temp[j,2],temp[j,3],alpha=100,
maxColorValue = 255))
polygon(c(data_Wahlbeteiligung$Wahlbeteiligung,
rev(data_Wahlbeteiligung$Wahlbeteiligung)),
c(data_Wahlbeteiligung[[paste(x,"_real",sep="")]],
rev(data_Wahlbeteiligung[[paste(x,"_uq_real",sep="")]])),
border=NA,col=rgb(temp[j,1],temp[j,2],temp[j,3],alpha=100,
maxColorValue = 255))
text(x=xtext[j],y=ytext[j],paste(ptext[j]),srt = angle[j],cex = 1)
j=j+1
}